Función arcoseno
Las funciones trigonométricas inversas son importantes y necesarias para el cálculo de los ángulos de un triangulo a partir de la medición de sus lados. Aparecen con frecuencia en las soluciones de ecuaciones diferenciales
Las 6 funciones trigonométricas básicas son, seno y su función recíproca el coseno, tangente y su función recíproca la cotangente y secante y su recíproca la cosecante. Estas no poseen inversa debido a que son funciones periódicas y por esta razón decimos que no son inyectivas. Se puede producir una excepción a esto cuando restringen los dominios, lo cual nos permite el hallazgo de la inversa.
La función seno
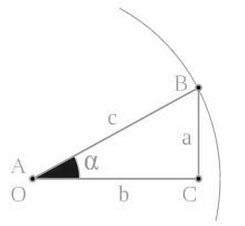
En trigonometría el seno de un ángulo en un triángulo rectángulo que se expresa y se puede definir como la razón entre el cateto opuesto y la hipotenusa:
sin(α)=a/c
O también como la ordenada correspondiente a un punto que pertenezca a una circunferencia goniométrica que se centre en el origen (c=1):
sin(α)=a
La función, y=sen x
Si se traza una recta horizontal se cortará la grafica en más de un punto. El codominio es [-1, 1]. Veamos ahora la gráfica siguiente,
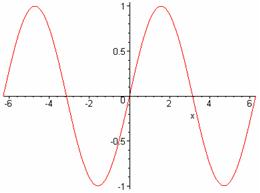
La función seno no es biyectiva, por lo cual no tiene inversa. Como hemos dicho antes, para hallar la inversa se procede a aplicar una restricción al dominio, así la función se vuelve inyectiva y sobreyectiva.
La función seno, codominio restringido
Si F(X)=sen x en el intervalo,
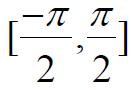
es creciente y entonces inyectiva o sea que existe la inversa y su recorrido es [-1, 1] su grafica estña representada en color azul,
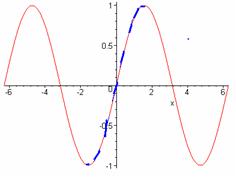
En trigonometría, el arcoseno está definido como la función inversa del seno. Si tenemos, arcsinα quiere decir que es el arco cuyo seno es alfa.
Suele denominarse arco a una cantidad que se expresa en forma de radianes, por esta razón las funciones inversas llevan el prefijo, arco.
Si y=senx, entonces la inversa se denota de las siguiente formas:

Por lo cual,
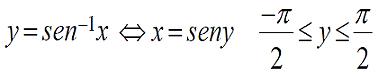
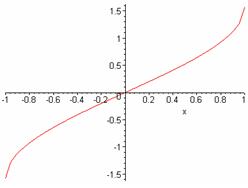
La función inversa de y=senx restringida la que vemos a continuación:
![]()
Su dominio es [-1, 1]
El recorrido es,
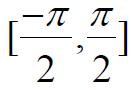
Esta gráfica es creciente y a la vez, es una función impar, ya que,
![]()
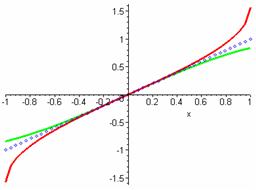
Las dos gráficas se manifiestan sobre la recta y=x
Para entender mejor el concepto de arcoseno, es importante recordar que las funciones trigonométricas son cíclicas. Esto significa que los valores de las funciones se repiten a intervalos regulares. Por lo tanto, el arcoseno de un número no es único. Por ejemplo, si el seno de un ángulo es 0.5, entonces el ángulo puede ser 30 grados o cualquier ángulo que sea 30 grados más o menos un múltiplo entero de 360 grados.
Además, es importante mencionar que el arcoseno es una función continua y diferenciable en su dominio. Esto significa que la función tiene un valor definido para cada número en su dominio, y que se puede calcular la pendiente de la tangente a la curva de la función en cualquier punto de su dominio.
En el campo de la física, el arcoseno se utiliza para calcular ángulos en diversas situaciones, como la determinación del ángulo de incidencia de la luz en un prisma, o el ángulo de lanzamiento necesario para que un proyectil alcance una distancia específica.
En matemáticas, el arcoseno se utiliza en la solución de ecuaciones trigonométricas. También se utiliza en la integración y diferenciación de funciones trigonométricas.
En conclusión, el arcoseno es una función matemática importante que se utiliza en una variedad de aplicaciones en matemáticas y física. Aunque puede ser un concepto desafiante de entender al principio, con práctica y estudio, se puede llegar a comprender y utilizar eficazmente esta función.

