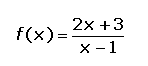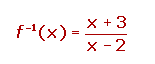Función inversa

Una vez que ya hemos visto la función compuesta, vamos a estudiar también la función inversa. Ya que la hemos mencionando anteriormente en las propiedades de las funciones compuestas.

En esta ocasión, estudiaremos el proceso para obtener la función inversa, además de ver algunos de los ejemplos más importantes de funciones inversas y cómo se representan.

DEFINICIÓN:

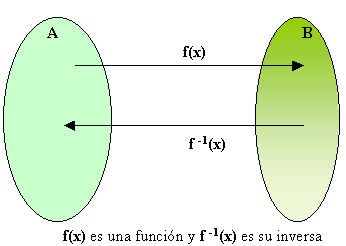
Se llama función inversa o recíproca de una función f a una nueva función cuyo dominio es la imagen de la función inicial, y su imagen es el dominio de la función inicial.

Es decir, si la función g es la función inversa de f, entonces se cumple que si f (b) = a, entonces g(a)=b.

PROPIEDADES

1. La primera propiedad coincide con la que habíamos visto anteriormente en la función compuesta. Si realizamos la función inversa de una composición de funciones obtenemos la composición de sus inversas permutando el orden de la composición:

2. Si hacemos la inversa de la inversa de una función, obtenemos la función inicial.

3. La composición de una función y su inversa nos da la función identidad.

4. La función inversa no siempre existe.

5. Si una función es continua también lo es su inversa y viceversa, si la inversa es derivable también lo será la función inicial.

6. Análogamente, si una función es derivable su inversa también lo es y viceversa.

GRÁFICA DE UNA FUNCIÓN INVERSA

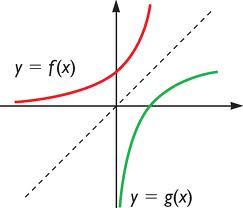
La gráfica de una función f, y la de su inversa g, son simétricas respecto a la bisectriz del primer y tercer cuadrante, es decir la recta y = x, como podemos ver en la siguiente imagen:

Por tanto si M(b,a) es un punto de f, y por tantosabemos que M´(a,b) será un punto de g, entonces las pendientes de las tangentes en M y en M´son inversas. Es decir si la pendiente de la tangente en M es m, entonces la pendiente de la tangente en M´ será 1/m.

Observación: Recordad que no es lo mismo la función inversa, que la inversa de una función.

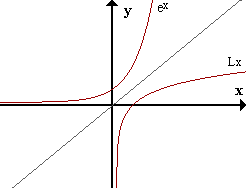
El ejemplo más conocido e importante de funciones inversas es la función exponencial y la función logarítmica. Y como podemos ver sus representaciones gráficas son simétricos respecto de la bisectriz del primer y tercer cuadrante:

PASOS PARA CALCULAR LA FUNCIÓN INVERSA

Para poder calcular la función inversa de una dada debemos seguir unos pasos:

1º. Realizamos un cambio de variable, cambiando y por x, y viceversa. Recordad que y=f(x).

2º. Una vez que ya hemos cambiado las variables, tenemos que despejar la variable y en función de x.

3º. El resultado final, es la función inversa que hemos buscado.

Por último vamos a realizar unos ejemplos en los que seguiremos los pasos (que son pocos y cortos) para obtener la función inversa en cada caso:

Ejemplo 1: Hallar la función inversa de f(x)=3x+5.

Vamos a seguir los pasos anteriormente descritos, antes que nada tendremos en cuenta que f(x)=y, por tanto empezaremos nuestros pasos a partir de la siguiente función: y=3x+5.

1º. Hacemos el cambio, obteniendo: x=3y+5.

2º. Despejamos y en función de x: 3y=x-5; y=(x-5)/3.

3º. Por tanto la función inversa es y=(x-5)/3.

Ejemplo 2: Calcular la siguiente función inversa:

1º. Hacemos el cambio de y por x:

2º. Despejamos la y:

3º. Finalmente, la función inversa es: