Periodicidad de una función

Vamos a estudiar hoy otro aspecto de las funciones que nos facilitan tanto su estudio como su representación: la periodicidad. Estudiaremos como reconocer una función periódica (que siempre será más fácil de forma gráfica) y estudiaremos sus características más importantes. Esta nueva característica permite una nueva clasificación de las funciones en funciones periódicas y no periódicas.

Este tipo de funciones que vamos a conocer hoy no nos son tan ajenas como nos puede parecer. Un ejemplo presente en nuestro día a día lo encontramos en las manecillas del reloj, o incluso las fases de la luna.

DEFINICIÓN

Definición formal: Diremos que una función f(x) es periódica cuando exista un número real T, tal que el valor de la función en el punto x coincida con el valor de la función en el punto x+T: f(x)=f(x+T). Llamamos periodo al número real T que nos indica cada cuanto se repite la función.

O dicho de otro modo, una función es periódica cuando el trazo de la función se repite cada cierto intervalo de la x siguiendo el mismo patrón.

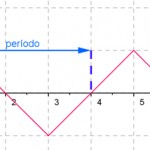Como podemos ver en la siguiente imagen, esta función es periódica porque su trazo se repite cada cuatro valores. Por tanto su periodo es 4: T=4. Si analizamos la función, podemos comprobar que f(1)=f(1+4)=f(5).

PERIODO DE FUNCIONES TRIGONOMÉTRICAS

Todas las funciones trigonométricas son periódicas.

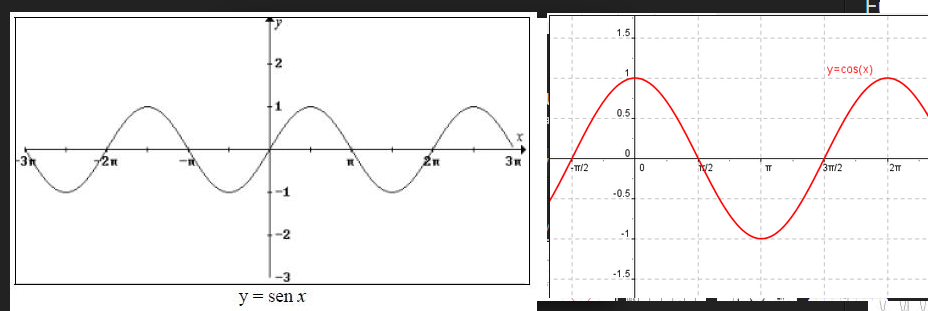
1. La función seno y la función coseno, f(x)=sen x y g(x)=cos x, son periódicas de periodo π.

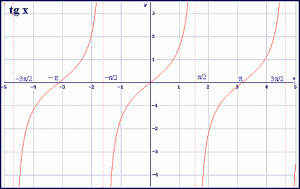
2. La función tangente f(x)=tg x es también periódica de periodo π.

Conocidos los casos principales en las funciones trigonométricas, podemos hallar el periodo de cualquier función teniendo en cuenta una serie de propiedades:

1- Dada una función periódica f(x) con periodo T, entonces la función que se obtiene al multiplicar la x por un número cualquiera (cambio de escala): g(x)= f(k∙x) también es periódica y el nuevo periodo se obtiene dividiendo el anterior por un número cualquiera: T»=T/k.

2- Dada una función periódica f(x) con periodo T, entonces la función que se obtiene multiplicando y sumando al término independiente por números reales g(x)=f( m∙x+n) también es periódica, y el nuevo periodo es el mismo que en el caso anterior: T»=T/m (no le afectan los cambios de origen).

Ejemplo: Hallar el periodo de la función f(x)=sen 2x.

Como ya hemos mencionado a principio, conocido el valor del periodo de la función f(x)=sen x, T= π. Entonces, aplicando la primera propiedad mencionada, el nuevo periodo es:

T»= π/2.

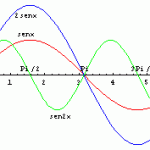
Como podemos apreciar en la siguiente imagen, se mantiene la misma forma, pero se reduce el periodo como podemos ver en el trazo en verde.

Si nos fijamos, no es lo mismo multiplicar por 2 el término independiente que la función, como podemos apreciar en el trazo azul.