Funciones acotadas

Hoy vamos a estudiar otra propiedad de las funciones (y/o series como veremos más adelante).

Vamos a estudiar en primer lugar cuando decimos que una función es acotada superiormente y cuando está acotada inferiormente, para finalmente poder establecer cuando una función es acotada.

FUNCIÓN ACOTADA SUPERIORMENTE

Definición: Decimos que una función está acotada superiormente si existe un valor K tal que no es superado por ningún valor de la función, es decir: f(x)≤K para todo valor de x perteneciente al dominio, como podemos ver en la siguiente imagen:

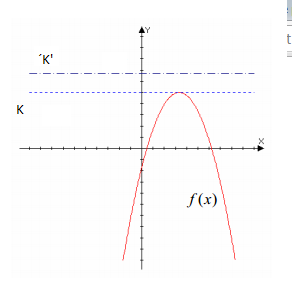
Al valor K se le denomina cota superior de f(x). Si lo interpretamos geométricamente quiere decir que toda la gráfica de la función se encuentra debajo de la recta y=K, como se puede apreciar en la imagen anterior.

Observación: Cualquier número que sea mayor que K, también es una cota superior de la función f(x). Por ejemplo, K» también es una cota superior de f(x), es decir, forma parte del conjunto de cotas superiores de la función.

FUNCIÓN ACOTADA INFERIORMENTE

Definición: Decimos que una función está acotada inferiormente si existe un valor k tal que no hay ningún valor de la función que sea inferior a k, es decir: f(x)≥k para todo valor de x perteneciente al dominio, como podemos ver en la siguiente imagen:

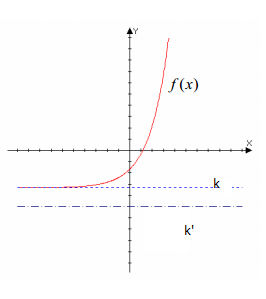
Al valor k se le denomina cota inferior de f(x). Análo al caso anterior, si lo interpretamos geométricamente, quiere decir que toda la gráfica de la función se encuentra por encima de la recta y=k, como se puede ver en la imagen anterior.

Observación: De igual forma al caso anterior, cualquier número menor que k, también es una cota inferior de f(x). Es decir, si k»<k, entonces, k' también es cota inferior de f(x), formando parte del conjunto de las cotas inferiores de la función.

FUNCIÓN ACOTADA

Definición: Decimos que una función está acotada, cuando está acotada superior e inferiormente. En caso contrario, diremos que no está acotada.

Por tanto una función está acotada cuando existe un valor K tal que la gráfica de la función no está por encima de él, y un valor k, tal que la gráfica de la función no está por debajo de él, es decir, k≤f(x)≤K, para todo x perteneciente al dominio de la función.

Si lo interpretamos geométricamente, quiere decir que la gráfica de la función se encuentra entre las rectas y=K e y=m.

Ejemplo: Un ejemplo claro de funciones acotadas son las funciones trigonométricas f(x)= sen x y f(x)= cos x. Ambas tienen como cota superior K=1, y como cota inferior k=-1.

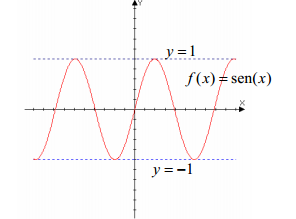
PROPIEDADES:

Sean f(x) y g(x) dos funciones acotadas, entonces:

1) La función resultante de la suma de las dos, y=f(x)+g(x) también es una función acotada.

2) La función resultante del producto de las dos, y=f(x)∙g(x) también es una función acotada.

3) Por tanto el conjunto de funciones acotadas tiene la misma estructura que el conjunto de funciones reales de variable real.

AMPLIACIÓN DE CONTENIDO

Para entender mejor el concepto de funciones acotadas, es útil considerar algunos ejemplos adicionales. Por ejemplo, la función f(x) = x^2 está acotada inferiormente, ya que no hay ningún valor de la función que sea inferior a 0. Sin embargo, no está acotada superiormente, ya que no existe un valor K tal que f(x) ≤ K para todo x.

Por otro lado, la función f(x) = 1/x está acotada superiormente pero no inferiormente, cuando se considera en el dominio x > 0. En este caso, la cota superior es 1 y no hay cota inferior.

Es importante destacar que la noción de acotación depende del dominio considerado. Por ejemplo, la función f(x) = 1/x no está acotada si se considera en todo el conjunto de los números reales, ya que no está definida en x = 0.

Además, es relevante mencionar que la existencia de cotas no garantiza la existencia de máximos o mínimos. Por ejemplo, la función f(x) = x no tiene ni máximo ni mínimo en todo el conjunto de los números reales, a pesar de que está acotada tanto superior como inferiormente.

Finalmente, es interesante observar que las propiedades de las funciones acotadas son útiles en muchos campos de las matemáticas. Por ejemplo, en el cálculo, el teorema del valor intermedio se basa en la propiedad de que toda función continua en un intervalo cerrado y acotado alcanza todos los valores intermedios entre su mínimo y su máximo. En el análisis real, la noción de función acotada es fundamental para la definición de la integral de Riemann. En la teoría de la medida, las funciones acotadas son esenciales para la definición de la integral de Lebesgue.