Función exponencial

Las funciones exponenciales son todas las funciones de la forma,

Aquí la base b, corresponde a una constante, mientras que el exponente corresponde a la variable independiente. Estas funciones son aplicadas en campos muy diversos que se relacionan con la biología, economía, administración, física, química e ingeniería.

La función exponencial, se conoce eneralmente como la función real, e elevado a x, donde e es representa al número de Euler, uno de los mas importantes y trascendentes números reales (los números reales incluyen tanto a los racionales como a los irracionales) con una cifra aproximada a 2.71828. Esta función tiene por conjunto de definición a la totalidad de los números reales, y como peculiaridad podemos decir que su derivada es correspondiente a la misma función. Se denota equivalentemente de la siguiente forma,

donde e es la base de los logaritmos naturales y es correspondiente a la función inversa del logaritmo natural. El logaritmo en base e es denominado logaritmo natural o también neperiano.

La derivada constituye una forma de representación de cómo una función se transforma (valor de la variable dependiente) mientras que su entrada propia(valor de la variable independiente) también se transforman. De forma no muy forma podemos decir que una derivada se puede ver como cuánto está cambiando el valor de una función en un punto dado (esto hace referencia a la velocidad de variación)

Generalmente se define una función real E(x) indicando que es del tipo exponencial en base a si posee una forma como la siguiente,

Entonces, obtenemos un conjunto de exponenciales, todos estos similares, dependientes de la base a que utilicen.

La función exponencial ex puede ser definida de manera formal de varios modos semejantes, como una serie sin fin. En especial se puede definir como una serie de potencias como sería la que sigue:

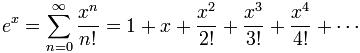
o como el límite de la sucesión:

La función exponencial y los exponenciales en base distinta a e, cumplen con las siguientes importantes propiedades

• e elevado a x, es su propia derivada. Es la única función con esa propiedad (sin tener en cuenta el producto de la función exponencial por una constante)

• Son las únicas funciones que se igualan con la derivada.

• exp(x+y)=exp(x).exp(y)

• exp(x-y)=exp(x)/exp(y)

• exp(-x)=1/exp(x)

• exp(0)=1

• su límite en – ∞ es 0, y en + ∞ es + ∞