Ecuación de la recta tangente
En este post vamos a estudiar una de las aplicaciones más importantes de las derivadas: la ecuación de la recta tangente y la recta normal; así como las diversas aplicaciones que nos podemos encontrar. Comenzaremos viendo la interpretación de la derivada, y a continuación los tres tipos de ejercicios que nos podemos encontrar:
-Interpretación geométrica de la derivada:
Como ya hemos visto anteriormente la definición de derivada, y a partir de la imagen que aparece en ese artículo:
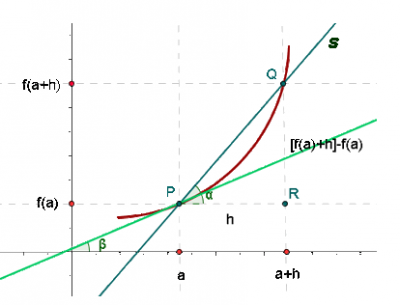
Podemos interpretar la derivada como la pendiente de la ecuación de la recta tangente de f(x) en el punto P(a,f(a)), que viene dada por la siguiente expresión: y-f(a)=f «(a) (x-a). Aunque siempre podemos utilizar la expresión conocida para cualquier recta y=mx+n, donde m=f » (a).
-Tipo 1: Hallar la ecuación de la recta tangente en un punto.
A partir de la función f(x) y dado un punto a en el que tenemos que calcular la recta tangente. Simplemente tenemos que calcular los datos que necesitamos para sustituir en la fórmula.
1º) Calcula cuanto vale la función en el punto a, es decir f(a)
2º) Calcular la pendiente. Para ello calcularemos la derivada y sustituiremos el valor de x por el punto, es decir m=f «(a).
3º) Sustituir en la fórmula de la ecuación de la recta tangente.
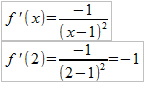
Ejemplo: Calcula la ecuación de la recta tangente a la función f(x)=1/(x-1) en el punto x=2.
1º) Hallamos f(2)=1/(2-1)=1.
2º) Calculamos la derivada, y a continuación sustituimos por 2.
3º) Sustituimos en la fórmula: y-f(a)=f «(a) (x-a) : y-1= -1(x-2)
-Tipo 2: Hallar la ecuación de la recta normal.
La recta normal es la recta perpendicular a la recta tangente, por tanto será de la forma: y-f(a)=- 1/f «(a) (x-a). Como podemos observar la pendiente en este caso es m»=-1/m, ya que las rectas son perpendiculares. Por tanto seguiremos los siguientes pasos:
1º) Hallamos la nueva pendiente: m»=-1/m
2º) Hallamos el valor de y=f(a).
3º) Sustituimos en la fórmula.
Ejemplo: A partir del ejemplo anterior hallar la ecuación de la recta normal en el punto x=2.
1º) Como la pendiente de la recta tangente era m=-1, la pendiente de la recta normal es: m»=-1/-1=1.
2º) Utilizamos el valor calculado de f(2)=1.
3º) Sustituyendo en la fórmula: Sustituyendo en la ecuación de la recta normal: y-f(a)=-1/f «(a)(x-a) obtenemos: y-1=1(x-2).
-Tipo 3: Hallar el punto en el que la recta tangente es paralela a una recta dada.
En este último caso, partimos de la función f(x) de la que nos piden hallar la recta tangente, y una recta paralela a la recta tangente. Para poder hacer este ejercicio, recordemos que dos rectas son paralelas cuando tienen la misma pendiente. Por tanto, para este tipo de ejercicios seguiremos los siguientes pasos:
1º) Hallamos la pendiente de la recta que nos dicen que es paralela.
2º) Calculamos la derivada de la función y la igualamos a la pendiente anterior: f «(x)=m.
3º) Resolviendo la ecuación anterior obtenemos el punto a donde hay que calcular la ecuación de la recta tangente.
4º) Hallamos f(a).
5º) Sustituimos en la fórmula de la recta tangente.
Ejemplo: Halla la ecuación de la recta tangente a la función f(x) tal que sea paralela a la recta 2x-y+3=0.
![]()
1º) Hallamos la pendiente de la recta, para ello despejamos en primer lugar la y: y=2x+3, luego la pendiente será m=2.
2º) Derivamos e igualamos a la pendiente: f «(x)=4x-4=2
3º) Resolvemos la ecuación:
6x-4=2 —> 6x=6 —>x=1=a
4º) Calculamos f(a)=f(1)=3-4+3=-4.
5º) Sustituimos en la fórmula: y-f(a)=f «(a)(x-a) —–> y+4=2(x-1)
