Función seno

La función seno es una función trigonométrica muy importante, que puede encontrarse en diversos campos de la ciencia. En física, por ejemplo, se utiliza para describir fenómenos periódicos como las ondas de sonido o las oscilaciones de un péndulo. En ingeniería, se utiliza para calcular la longitud de los lados de un triángulo en función de sus ángulos. Y en matemáticas, es una de las funciones básicas que se utilizan para resolver ecuaciones trigonométricas.

Podemos definir a la función seno como:

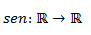
Es decir, que pertenece al conjunto de los números reales, y su solución es otro número real, que se expresa como f(x)= sen(x), es por tanto, una aplicación de la razón trigonométrica seno a una variable independiente, que se suele expresar en radianes. En otras palabras, la función seno toma un ángulo (en radianes) y devuelve la longitud del lado opuesto en un triángulo rectángulo unitario.

Cabe destacar que los valores del seno siempre variarán entre -1 y 1, como se puede ver en la siguiente gráfica:

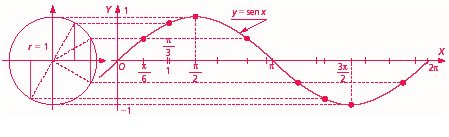
Además, se puede ver que es una función impar, ya que sus elementos opuestos tienen imágenes opuestas (el seno de 30 es 1/2, y el de -30 es -1/2) y también continua en todo su recorrido. Esto significa que la función seno es simétrica con respecto al origen, es decir, que si dibujamos la gráfica de la función seno, veremos que es la misma si la miramos desde arriba o desde abajo.

**Nota: para recordar que tiene imágenes opuestas, podéis quedaros con la idea de que es como una ola, que viene y va, estrellándose contra la arena, para volver a surgir de nuevo.

Si nos fijamos atentamente, veremos que el seno no es más que el cateto opuesto al ángulo, partido de la hipotenusa de un triángulo rectángulo. Si vamos rotando ese triangulo imaginario en esa circunferencia, nos irá dando los distintos valores de los ángulos del seno. Esta es la base de la definición de la función seno y es una de las razones por las que es tan útil en trigonometría.

Os dejo la tabla de valores de la función seno, como resultado de la rotación que acabáis de ver, es importante que la memoricéis pues os hará falta para los temas de trigonometría.

¿Y por qué pi vale 180? No es porque si. Pi representa la relación matemática entre la longitud de una circunferencia y la longitud de su diámetro. No quiero enrollarme, así que lo dejaremos ahí, ya habrá tiempo de explayarse en nuestro querido pi. Pi es una constante matemática que se encuentra en muchas áreas de la matemática y la física, y es uno de los números más importantes en el mundo de las matemáticas.

Ejemplos:

Halla el seno del ángulo del siguiente triangulo rectángulo sin usar la calculadora:

 

 

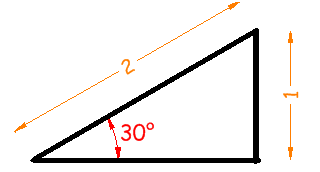
Como sabemos:

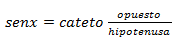
Por tanto:

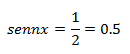
Como habrás notado, la función seno es una herramienta muy útil en una amplia gama de aplicaciones. No solo es fundamental en trigonometría, sino que también juega un papel crucial en muchos otros campos de la matemática y la física. Así que, ya sea que estés estudiando matemáticas, física, ingeniería o cualquier otra disciplina que requiera el uso de trigonometría, entender la función seno y cómo usarla correctamente es esencial.