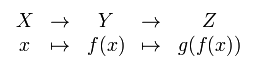Función compuesta

Aquí está el artículo actualizado con el nuevo contenido:

Vamos a estudiar un nuevo concepto del Análisis Matemático: la función compuesta.

Una función compuesta es una función que está formada por la composición de dos funciones, es decir, la función resultante de aplicar a x una función en primer lugar y a continuación a este resultado le aplicamos una nueva función.

La forma en que denotamos la función compuesta es un pequeño círculo entre las dos funciones o g(f(x)), que quiere decir que en primer lugar se aplica la función f, y al resultado la función g.

DEFINICIÓN

Definición formal: Dadas dos función f y g, tales que f: X → Y y g: Y → Z, donde es necesario que la imagen de f esté contenida en el dominio de g, se define la función compuesta de f y g : g(f(x)) ( tened mucho cuidado ya que para leerlo o nombrarlo se hace al revés de como se escribe ) como (g∘ f)(x)=g(f(x)), para todo x perteneciente a X. Lo podemos representar como:

Hay que señalar que la función compuesta definida de esta forma está bien definida ya que cumple las dos condiciones necesarias: la de existencia y la de unicidad.

-Condición de existencia: Para todo valor de x del dominio de f podemos halla (x,f(x)), y para cualquier elemento y=f(x) del dominio de g podemos halla (y,g(y))=(f(x),g(f(x))). Por lo tanto, podemos decir que g(f(x) cumple la condición de existencia. Veamos ahora que pasa con la condición de unicidad.

-Condición de unicidad: Como tanto f como g son funciones que están bien definidas, para cada valor de x existe un único valor f(x) (ya que en caso contrario no sería una función), y para cada f(x) también existe un único valor de g(f(x)).

Con lo cual queda demostrado que la función compuesta está bien definida.

Por ejemplo, sea f(x)=3x-1 y g(x)=1/x, entonces g(f(x))=1/(3x-1).

PROPIEDADES DE LA FUNCIÓN COMPUESTA

1. La función compuesta cumple la propiedad asociativa: h∘ (g∘ f)= (h∘ g)∘ f

2. La función compuesta no es conmutativa: (g∘ f) ≠ (f∘ g)

3. Tiene elemento neutro que es la función identidad I(x)=x: (I∘ g)=(g∘ I)=g

4. La composición de una función con su inversa nos da la función identidad, es decir, existe elemento simétrico, el cual es la función inversa:

5. Si realizamos la función inversa de una composición de funciones obtenemos la composición de sus inversas permutando el orden de la composición:

6. Si f es derivable en x y g es a su vez derivable en f(x), entonteces existe la derivada de la función compuesta y se calcula utilizando la conocida regla de la cadena:

(g∘ f)´(x)=g´(f(x))f´(x)

Además de las propiedades mencionadas, es importante destacar que las funciones compuestas tienen aplicaciones prácticas en diversas áreas de la matemática y otras disciplinas. Por ejemplo, en la física, las funciones compuestas se utilizan para describir fenómenos donde una cantidad depende de otra, la cual a su vez depende de una tercera. En la economía, pueden modelar situaciones donde una variable económica depende de otra, que a su vez depende de una tercera variable.

Otra propiedad interesante de las funciones compuestas es su comportamiento bajo transformaciones lineales. Si f y g son funciones lineales, entonces su composición también es una función lineal. Esto se puede ver claramente si consideramos que una función lineal tiene la forma f(x) = ax + b y g(x) = cx + d. La composición g(f(x)) será entonces g(ax + b) = c(ax + b) + d = acx + bc + d, que es una función lineal.

Por último, es útil mencionar que las funciones compuestas también juegan un papel crucial en la teoría de sistemas dinámicos y en el estudio de ecuaciones diferenciales. En estos campos, la composición de funciones puede representar la evolución de un sistema a lo largo del tiempo, donde cada función en la composición representa una etapa diferente del proceso.

Vamos a realizar un ejercicio adicional para reforzar estos conceptos:

Ejemplo: Dadas las siguientes funciones h(x)=x^2 y k(x)=sqrt(x), realizar las siguientes composiciones indicadas:

a) Hallar (k∘ h).

b) Hallar (h∘ k). ¿Qué podemos decir en relación al apartado anterior?

c) Sabiendo que la inversa de h es sqrt(x), comprobar que se cumple la propiedad número 4.

a) En primer lugar nos están pidiendo la composición de h y k (recordad que se tenía que leer al revés)

(k∘ h)(x)=k(h(x))=k(x^2)=sqrt(x^2)=|x|

Como podéis observar, en primer lugar sustituimos el valor de h(x), y a continuación, hemos sustituido el valor de x en la función k por el valor de h(x).

b) Siguiendo el mismo procedimiento calculamos ahora h compuesto con k:

(h∘ k)(x)=h(k(x))=h(sqrt(x))=(sqrt(x))^2=x

Como podemos ver, es distinta a la calculada en el apartado a, como era de esperar, ya que no son conmutativas.

c) Calculamos ahora la composición de h con su inversa:

(x)=h(sqrt(x))=(sqrt(x))^2=x

Como se puede observar, se cumple la propiedad número 4, ya que la composición de una función con su inversa nos da la función identidad.