Evolución de los números

A lo largo de la historia el ser humano siempre ha tenido la necesidad de contar, de expresar operaciones mercantiles y de resolver otros problemas que han ido surgiendo en el desarrollo de las matemáticas.

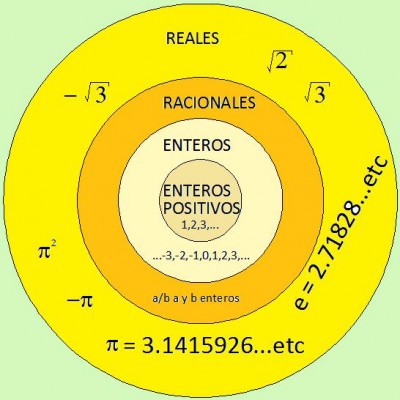
Analizaremos la evolución de los diversos conjuntos, de tal forma que cada uno de ellos esté contenido en el siguiente. No obstante, la evolución de estos números puede ser que coincida en el tiempo.

Los números naturales:

Desde el comienzo de la humanidad las diferentes culturas han empleado diversas formas de contar, ya sea utilizando piedras, muescas en palos e incluso los dedos de las manos y los pies. Sin embargo, no fue hasta el siglo IX d.C, gracias a Al-Khwarizmi cuando se adopta el sistema de numeración hindú. No obstante, en Europa tendremos que esperar hasta el siglo XIII para que los números naturales lleguen. Estableciéndose de manera formal en el siglo XIX gracias a Peano, a quien debemos la definición axiomática de los números naturales.

Los números enteros:

La solución de ecuaciones del tipo x+a=b, donde a>b, no tienen cabida en el cuerpo de los números naturales. Necesitamos ampliar el conjunto y definir de esta forma los números negativos. Estos números surgieron por la necesidad de operar con cantidades negativas, sobre todo en las operaciones comerciales. Los primeros en introducir los números negativos fueron los hindúes, en concreto, Brahmagupta. A Europa llegan a finales del siglo s.XV gracias al matemático francés Nicolas Chuquet. Si embargo, no fue hasta finales del siglo XIX cuando Weierstrass perfila el modelo de los números enteros, definiéndolos como clases de equivalencias de paras de números naturales.

Los números racionales:

A la hora de resolver la ecuación ax=b, tal que b no es múltiplo de a (es decir, a no es divisor de b), no existe solución en los números enteros. La necesidad de fraccionar la unidad nos lleva a la definición de las fracciones. Aunque se trabaja con ellas desde la antigüedad, pero con notaciones complicadas. Los babilonios comenzaron a utilizar la notación decimal, dividiendo la unidad en potencias sucesivas de 60. Pero fueron los árabes quien establecieron la barra horizontal para separar el numerador y el denominador.

Los números reales:

Aparece un nuevo obstáculo que hace que el cuerpo de los números racionales se quede pequeño, como el de hallar lo que mide la diagonal de un cuadrado de lado 1, o el resultado de la ecuación x al cuadrado igual a 2. Este descubrimiento se produce gracias a la escuela pitagórica, y recibieron el nombre de inconmensurables. No obstante, no fue hasta la llegada del Renacimiento, cuando los matemáticos europeos aprovecharon el sistema decimal, para definir los números irracionales como aquellos números que tienen infinitas cifras decimales.

Los números complejos:

Por último, como obstáculo final nos encontramos con un nuevo problema, ¿qué ocurre cuando al resolver una ecuación de segundo grado o superior obtenemos una raíz cuadrada negativa? Hasta entonces, esta ecuación no tiene solución (de hecho no tiene solución real). Aunque se comenzó a trabajar con estos números como si se trataran de números normales, ya que cumplían una serie de condiciones. El carácter esotérico de estos números se fue eliminando, sobre todo con la obra de Cardano en 1545 «Arg Magna». Sin embargo, fue Euler el que estableció la notación que ahora conocemos, para denotar la raíz de menos uno como i.