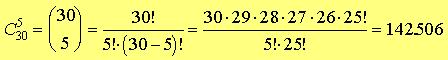Combinaciones ordinarias
Como ya sabemos, la combinatoria es la parte del álgebra que se encarga del estudio de los grupos que pueden formarse con determinados elementos, distinguiéndose entre ellos el número de elementos, su tipo y el orden. Las agrupaciones formadas pueden ser las variaciones, permutaciones o las combinaciones. Estas últimas serán las que estudiaremos en este artículo.
Antes de adentrarnos en el tema, podemos dar un sencillo ejemplo, el cual nos dará una visión más clara de lo que son las combinaciones y nos ayudará a comprender mejor. Por ejemplo si tenemos una ensalada de frutas tenemos una combinación de frutas, podría ser una combinación de manzanas, naranjas y bananas. O podemos decir también naranjas, bananas y manzanas, etc. Es evidente entonces que no importa en qué orden pusimos las frutas, ya que siempre será la misma ensalada.
Llamamos entonces combinaciones ordinarias o sin repetición de m elementos, tomados de n en n, a las distintas agrupaciones que pueden formarse con esos m elementos de manera tal que en cada grupo puedan entrar n de ellos. De este modo se diferencia un grupo de otro, por lo menos en uno de sus elementos. El número de combinaciones ordinarias de m elementos lo notaremos como Cn,m.
Si A es un conjunto con n elementos y m un natural menor o igual que n.
Llamaremos combinación ordinaria o combinación de m elementos de A a todo subconjunto de m elementos de A.
Debemos tener en cuenta a los elementos que tiene el subconjunto independientemente del ordenamiento de estos , o sea que si hablamos de combinaciones, dado A={a,e,i,o,u} se razona como el mismo subconjunto {a,e} que {e,a}. Lo que nos importa entonces es la naturaleza de los elementos y no el ordenamiento de estos. Podemos calcular las combinaciones de la forma siguiente:
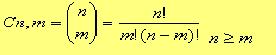
Veamos algunos ejemplos:
Pedro tiene 9 amigos y quiere invitarlos a almorzar, pero sólo puede invitar a 6 de sus amigos simultáneamente. ¿Cuántos grupos diferentes de invitados puede tener?
En este problema lo que en verdad queremos saber es cuantos grupos diferentes podemos establecer independientemente del orden en que se elijan a los invitados. Para esto podemos proceder de la siguiente forma:
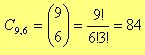
Podemos tener entonces 84 grupos distintos de invitados.
Cuantos grupos de 5 estudiantes pueden constituirse con los treinta estudiantes de una clase. Tengamos en cuenta que un grupo es diferente de otro si se diferencia al menos por un alumno. Aquí no importa el orden ya que son grupos de alumnos. No puede haber dos estudiantes iguales en un grupo, indudablemente. Siendo así, se pueden formar 142506 grupos desiguales: