Variaciones ordinarias
Por análisis combinatorio, hacemos referencia a aquella parte del álgebra que se encarga del estudio de los grupos que se forman con elementos dados, diferenciándose entre si, por el número de elementos que se incorporan en cada grupo, por el tipo de elementos y por el orden de su colocación.
El número de elementos del cual se dispone para formar las diferentes agrupaciones se denomina base, mientras que el número de elementos que intervienen en cada agrupación se denomina orden. Se llaman monarias a las agrupaciones de orden 1 y las agrupaciones de orden 2 binarias, a las de 3 ternarias, etc.
Los m elementos que se tienen para formar los grupos pueden ser distintos aunque también se pueden encontrar algunos que sean iguales. En caso de que sean distintos, las agrupaciones formadas se llamarán ordinarias. En el segundo caso se llamarán agrupaciones con repetición. Según estos criterios que se utilizan para la formación, las agrupaciones pueden tener tres formas que serían, variaciones, permutaciones o combinaciones.
Veamos a continuación que es entonces una variación ordinaria. Sea A un conjunto con n elementos desiguales y m natural y menor que n. Llamaremos variaciones ordinarias de m elementos de A a todas aquellas posibles agrupaciones ordenadas que se puedan hacer de los m elementos. El número de variaciones ordinarias viene dado de la siguiente forma:
Vn,m=n(n-1)(n-2)…..(n-m+1)
Como podemos ver, las variaciones ordinarias se representan con el símbolo Vm, n.
También podemos calcular las variaciones mediante factoriales
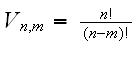
Como características de las variaciones ordinarias podemos decir que dos grupos son distintos si difieren en determinado momento en algún elemento o en su orden de colocación. Tampoco se repiten los elementos. El orden de estos influye.
Además, es importante destacar que las variaciones ordinarias son una herramienta fundamental en el análisis combinatorio, ya que permiten calcular la cantidad de formas en que se pueden ordenar los elementos de un conjunto. Este concepto es de gran utilidad en diversas áreas, como la informática, la estadística, la física y la economía, entre otras.
Por ejemplo, en informática, las variaciones ordinarias son utilizadas para calcular la cantidad de posibles contraseñas que se pueden generar con un determinado conjunto de caracteres. En estadística, se utilizan para calcular la probabilidad de que ocurran ciertos eventos. En física, se utilizan para calcular la cantidad de formas en que se pueden ordenar las partículas en un sistema. Y en economía, se utilizan para calcular la cantidad de formas en que se pueden distribuir los recursos en un sistema económico.
Veamos ahora un ejemplo:
¿Cuántos números de tres cifras desiguales podemos formar con 1, 2, 3, 4, 5,6?
Para resolver esto, vamos a formar subconjuntos de tres elementos desiguales, en los cuales nos importa que el orden 123. Difiere de 321. Por lo cual se van a formar:
![]()
Veamos ahora otro ejemplo del mismo tipo.
¿Cuántos números de tres cifras diferentes se puede formar con los dígitos: 1, 2, 3, 4, 5?
m = 5n = 3 m ≥ n
No entran todos los elementos. De 5 dígitos entran únicamente 3.
Como ya hemos dicho, sí importa el orden. Son números distintos el 123, 231, 321.
No se repiten los elementos. El enunciado nos pide que las cifras difieran.
El resultado es este:
![]()
En resumen, las variaciones ordinarias son una herramienta muy útil en el análisis combinatorio, permitiendo calcular la cantidad de formas en que se pueden ordenar los elementos de un conjunto. Su aplicación en diversas áreas demuestra su relevancia y utilidad en la resolución de problemas complejos.
