Permutaciones ordinarias
La combinatoria es una rama de matemática que trata el estudio de conjuntos finitos de objetos que satisfacen criterios específicos y que se ocupa especialmente del conteo de los objetos de dichos conjuntos. O sea que es una parte del álgebra que se encarga de estudiar los grupos que se forman distinguiéndose entre ellos el número de elementos que conforma cada grupo, el tipo de estos elemento y su orden.
Un problema combinatorio consiste usualmente en establecer una regla sobre como deben ser las combinaciones y determinar luego cuantas de estas existen que cumplan la regla. Las agrupaciones pueden ser de tres tipos, variaciones, combinaciones y las permutaciones. Los elementos de las agrupaciones pueden ser distintos, de ser así se llaman ordinarios o bien pueden ser iguales que serían las agrupaciones con repetición. Veamos a continuación que son las permutaciones ordinarias que también pueden llamarse permutaciones sin repetición de n elementos.
Dados m objetos, llamaremos permutaciones ordinarias de esos m elementos a las variaciones ordinarias de los mismos tomados m a m, o sea , a los diferente grupos que con ellos pueden constituirse, de manera que entrando todos ellos en cada grupo, se diferencie un grupo de otro simplemente en el ordenamiento de los elementos. Al número de permutaciones ordinarias de n elementos lo representaremos por Pn. Por tratarse de un caso particular de las variaciones, la fórmula que utilizaremos en los cálculos y que nos dará el número de permutaciones con m elementos Pm será:
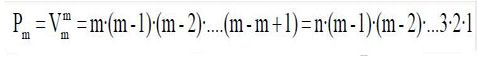
Si invertimos el orden de los factores:
Una característica importante de este tipo de agrupación es que se toman todos los elementos del conjunto. También se puede destacar que si importa el orden de los elementos ya que un grupo se diferencia de otro solamente en el orden de colocación de dichos elementos. Podemos observar también que las permutaciones coinciden entonces con las variaciones de n elementos tomados de n en n.
Vn,n = Pn
Veamos algunos ejemplos resueltos de permutaciones ordinarias:
Ocho personas guardan cola en una panadería para comprar pan. ¿De cuántas formas diferentes se pueden colocar en la cola?
¿ De cuántas formas distintas se pueden fotografiar 5 amigos frontalmente en línea recta?
