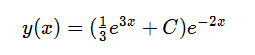Ecuaciones diferenciales ordinarias

Vamos a introducir hoy un nuevo concepto de ecuación, la ecuación diferencial, que como su nombre indica es una ecuación en la que intervienen las derivadas de una o de más funciones que desconocemos.

Empezaremos viendo los casos más sencillos, las ecuaciones diferenciales ordinarias, en las que aparece derivadas respecto a una única variable independiente; dejando para otro día el estudio de las ecuaciones en derivadas parciales.

Un ejemplo de ecuación diferencial ordinaria es : y´=3xy-2, donde y=f(x) e y´es la derivada de y en función de x: y´=dy/dx.

Veamos ahora algunos conceptos necesarios para trabajar con este tipo de ecuaciones:

-Orden de una ecuación: viene dado por la derivada más alta de la ecuación.

-Ecuación diferencial lineal: es una ecuación diferencial en la que ni la función ni las derivadas están elevadas a potencias distintas de 0 o 1; en cada coeficiente que multiplica a las derivadas sólo interviene el término independiente. Viene dada por la siguiente expresión:

-Ecuación homogénea: es la ecuación que se obtiene cuando g(x)=0.

-Solución general: como su nombre indica es la más general y genérica, y suele tener una o varias constantes.

-Solución particular: se obtiene cuando le damos valores a las contantes de la solución general.

MÉTODO DE SEPARACIÓN DE VARIABLES

Vamos a estudiar en primer lugar cómo resolver ecuaciones diferenciales homogéneas, utilizando el método de separación de variables. Veamos cuales son los pasos que hay que seguir a partir de un ejemplo:

Resolver la ecuación diferencial y´-2x/y = 0:

1º. En primer lugar escribimos de la forma y´=2x/y.

2º. Dejamos en el primer término todo lo que lleve y, y en el segundo lo que lleve x, quedando de la siguiente forma: yy´=2x.

3º. Teniendo en cuenta que y´=dy/dx, reescribimos la ecuación anterior: y dy/dx=2x,

4º. Pasamos el dx multiplicando al otro lado: ydx=2xdx.

5º. Hacemos la integral en ambos miembros de la igualdad obteniendo:

6º. Despejamos y, obteniendo nuestra solución general de la ecuación homogénea:

En el caso particular de las ecuaciones diferenciales ordinarias, en primer lugar siempre tenemos que dejarla de la siguiente forma: y´+P(x)y = 0; y siguiendo el procedimiento anterior, si queremos comprobarlo, la solución particular será: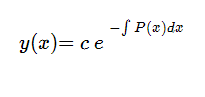

Ejemplo: Hallar la solución de la siguiente ecuación:

1º. La solución de la ecuación homogénea será:

2º. En esta solución sustituimos c, por c(x), y sustituimos en la ecuación inicial.

3º. Una vez que hemos sustituido, derivando previamente y(x), despejamos c´(x):

4º. Finalmente, integramos para obtener c(x), y sustituimos en la expresión obtenida en 2. Nuestro resultado será:

Hasta aquí ha llegado nuestra introducción al mundo de las ecuaciones diferenciales. Al igual que ocurre con las ecuaciones, también existen sistemas de ecuaciones diferenciales, que dejaremos también para otro día con más calma.