Raíz de una función

Cuando se habla de raíces en matemáticas, se refiere a todo elemento de una función f(x) tal que:

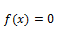
La raíz también puede referirse a un número de la forma:

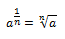
Que no es otra cosa que la raíz de un polinomio de la forma: (x^n )–a. Un ejemplo de ello sería la raíz cuadrada, la raíz cúbica, etc.

Es necesario destacar que, dichas soluciones, se deben encontrar dentro de un rango posible, que llamamos Dominio de la función. Dicho domino, puede comprender tanto los números reales como los irracionales.

Además, es importante tener en cuenta que las raíces de una función no siempre son números reales. En algunos casos, las raíces pueden ser números complejos. Los números complejos son números que incluyen la unidad imaginaria ‘i’, que es la raíz cuadrada de -1. Por ejemplo, la función f(x) = x^2 + 1 tiene dos raíces complejas, i y -i. Estas raíces no pueden representarse en la línea de números reales, pero son fundamentales en muchos campos de las matemáticas y la física.

Veamos un ejemplo gráfico:

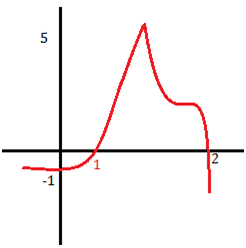
Llamemos a está curva: y=f(x)

En ella vemos, que para cada valor de x (eje de abscisas, el horizontal) le corresponde un valor de y (eje de ordenadas, el vertical). La curva toma pues, diferentes valores con cada nueva variable que añadimos. Pero observamos que, hay casos, en los que la función corta al eje x. Eses «cortes» son debido a que allí la función vale cero, o siendo más concretos, que el valor de «y» es cero.

Además de las raíces, existen otros elementos importantes en el estudio de las funciones, como los puntos de inflexión y las asíntotas. Un punto de inflexión es un punto en el que la curva cambia su concavidad, es decir, pasa de ser cóncava a convexa o viceversa. Por otro lado, una asíntota es una línea recta a la que la curva se acerca cada vez más, pero nunca llega a tocar.

Para entenderlo mejor, mirémoslo del revés, pensemos que tenemos un valor de «y», -1, y para este caso equis vale cero. Como observáis, la función no desaparece, simplemente, sigue en línea recta por ese punto solamente.

Tenéis que pensar en las raíces como los puntos de referencia de las funciones, ya que, puede ser difícil conocer todos los puntos, pero sin los puntos de corte con los ejes, o raíces de la función, es imposible representarlas. Esto os va a venir bien cuando os pongan ejercicios y os pidan dibujar una función, por lo que ya sabréis, que para hallar los puntos de corte, os acordáis de que son las raíces de la función, es decir, cuando la función se hace cero.

Finalmente, es importante mencionar que existen diferentes métodos para encontrar las raíces de una función. Algunos de estos métodos son el método de bisección, el método de Newton-Raphson y el método de la secante. Cada uno de estos métodos tiene sus ventajas y desventajas, y su elección depende de la naturaleza de la función y de las necesidades específicas del problema a resolver.