Función real de variable real

Llamamos función real de variable real, a toda función que esté definida como un subconjunto D de los números reales, en un conjunto R de los números reales por lo que a cada elemento x de D le corresponde únicamente un solo elemento Y de R. Cualquier expresión del tipo y=f(x) representa una función real de variable real.

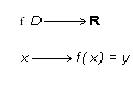
Una función real está definida generalmente por una ley o razonamiento que se puede expresar con una fórmula matemática. La variable x recibe el nombre de variable independiente y la variable Y o f(x) variable dependiente o imagen.

Para que se defina correctamente una función es necesario que se determine el conjunto inicial o el dominio de la función, la imagen de la función o el conjunto final y la regla por la cual se establece a cada elemento del conjunto origen o un solo elemento del conjunto imagen. Entonces por ejemplo una función que se define como se muestra a continuación, asigna su cuadrado a cada número real.

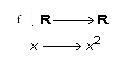
También Posee todos los números reales por campo de existencia o conjunto origen. Ya que dado un número real x, es posible calcular su cuadrado, siendo el resultante otro número real. Por conjunto de imagen posee todos los números reales positivos. Esto se da, ya que el cuadrado de un número es positivo siempre.

lm(f)=R+

Un campo de existencia está conformado por todos los números reales x, para los cuales su imagen se define mediante la función f. Si queremos encontrar el capo de existencia de la función f definida por:

Asignaremos a cada número x el valor 1/(x-2) expresión que está definida para todos los números reales, a excepción de aquellos que anulen el denominador, ya que la expresión 1/0 no es un número real. Entonces el denominador x-2 se anulará si x=2. Por lo tanto el campo existencia de la función es R – {2}.

El dominio de una función es el conjunto de números reales donde está definida la función. Puede estar determinado por la naturaleza del problema.

Por ejemplo si estudiamos el área de un cuadrado, el dominio estará formado por números reales positivos. La función que representa esto sería f(x) igual a x al cuadrado.

Podemos observar que en principio no habría ningún inconveniente en calcular esta función, como imagen de un número real negativo por ejemplo:

f(-8)=(-8)2=64.

Pero el dominio podría ser R. por lo cual vendría determinado, por la naturaleza del problema que no admite cuadrados negativos.

Otro ejemplo sería con la sucesión de números reales (an)= (-n2+18) . En una función f(n)=-n2+18.

Aquí en principio no tenemos inconveniente en calcular la imagen de un número real. Pero la propia definición nos hará considerar que son posibles solo las imágenes de números naturales.

Como último ejemplo por la expresión algebraica que define el criterio tenemos que tener en cuenta tres aspectos fundamentales. El radicando de una raíz par que debe ser positivo. En caso de una división el divisor debe ser distinto de cero y por último que la función logaritmo solo admite valores estrictos mayores que cero. Veamos algunos ejemplos:

Aquí no aparecen cocientes, raíces o logaritmos en los cuales intervenga la variable x, por lo cual podemos calcular la imagen de cualquier número real, entonces D(f)=R.

Ahora veamos otro ejemplo :

En este caso, como el radicando de una raíz de índice par debe ser positivo, debemos requerir que :

En el ejemplo que se muestra a continuación, los puntos que no pertenecen al dominio son los que se anulan al denominador que son x-1=0 y x=1, por lo cual el dominio de f serán todos los números reales a excepción de 1: D(f)=R{1}.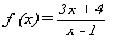

A continuación tenemos el último ejemplo : en el cual se deberá establecer lo siguiente: