Función elemental

Una función elemental es aquella que se puede construir a partir de una cantidad finita de exponenciales, logaritmos, constantes, una variable, raíces de ecuaciones mediante composición y combinaciones, mediante la utilización de las cuatro operaciones elementales que serían, suma, resta, multiplicación y división. Las funciones trigonométricas y sus inversas están dentro del grupo de funciones elementales puesto que se pueden obtener por medio del uso de variables complejas y sus relaciones entre las funciones trigonométricas, las funciones exponenciales y el logaritmo.

Un ejemplo de una función que no es elemental es la función error. Dicha función es utilizada en el campo de la probabilidad, la estadística y las ecuaciones diferenciales parciales.

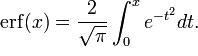
Se puede demostrar lo anterior por medio del el algoritmo de Risch.

La concepción de lo que conocemos como funciones elementales fue desarrollada por Joseph Liouville entre 1833 y 1841. Durante la década de 1930 Joseph Fels Ritt fue un precursor en el sistema algebraico de las funciones elementales.

Las funciones elementales se pueden clasificar como funciones polinómicas, tanto lineales como cuadráticas, funciones a trozos, valor absoluto de funciones y funciones racionales.

Funciones polinómicas

Una función Y= f(x) decimos que es lineal cuando:

F(x) es un polinomio de primer grado. Veamos algunos ejemplos de funciones lineales:

Una función cuadrática o función de segundo grado es una función polinómica que se define mediante un polinomio de segundo grado:

a, b y c son constantes y a es distinto de 0.

Funciones a trozos

Son funciones definidas por distintos criterios, según los intervalos que se consideren. Veamos un ejemplo:

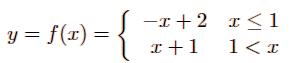
Podemos decir que posee dos ramas:

La rama correspondiente a –x+2 se define cuando x es un valor menor o igual a 1.

La rama x+1 se define cuando x toma un valor mayor que 1.

Si calculamos los valores de la función debemos sustituir en la rama correspondiente el valor de x.

Valor absoluto de funciones

El valor absoluto de un número es el mismo si es positivo, pero cambia de signo si es negativo. Por ejemplo:

A continuación estudiaremos y representaremos la siguiente función:

Y=│X│

De forma general con el valor absoluto las funciones resultarán definidas a trozos:

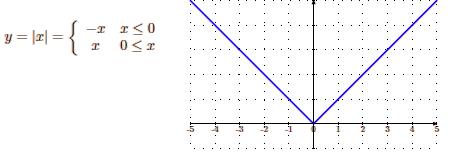
Función racional

Una función y=f(x) decimos que es una función racional si:

Es entonces un cociente de polinomios p(x) y Q(x). Siendo así, su dominio es la totalidad de los números reales exceptuando los números que anulan al denominador.

Dom= R- (raíces del denominador)

Veremos ahora representada una de las funciones racionales mas sencillas y=1/x con la realización de unas tablas de valores. Observaremos allí que para valores cercanos a 0 la función tomará valores muy grandes:

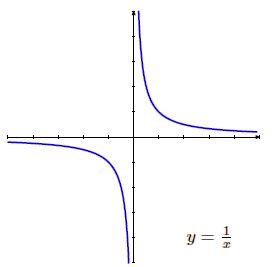
Podemos apreciar como la función se aproxima al eje Oy el cual es una asíntota vertical. Aproximandose al eje Ox es una asíntota horizonal.