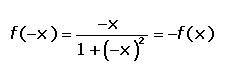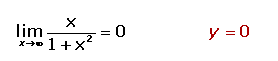Representación de funciones

Hemos visto en varias ocasiones como representar algunas de las funciones elementales: las racionales, las radicales, polinómicas (parábolas)… Hoy vamos a dar los pasos que hay que llevar a cabo para realizar el estudio y representación de cualquier función.

Estos pasos son necesarios para llevar a cabo la representación, aunque no son siempre necesarios todos ellos.

1º) Estudiar el dominio de una función:

El dominio son los todos los valores de x que puede tomar nuestra función, dependen del tipo de función que estemos estudiando:

a) Si f(x) es un polinomio el dominio son todos los números reales: Dom f(x)=R.

b) Si f(x)=P(x)/Q(x), el dominio serán todos los valores de x que no anulen el denominador: Dom f(x)=R-{Q(x)=0}.

c) Si f(x) es una raíz de orden, el dominio serán los valores que hagan que lo de dentro de la raíz sea mayor o igual a cero (ya que no existen las raíces cuadradas de números negativos); si f(x) es una raíz de orden impar el dominio son todos los números reales.

d) Si f(x) es un logaritmo, el dominio está formado por todos los valores que hacen que lo dentro sea mayor que cero (el logaritmo de 0 y de los números negativos no existe).

2º) Puntos de corte con los ejes:

Estudiar los puntos en los que la función corta a los ejes de coordenadas:

-Cortes con el eje abscisas (OX): por tanto y=0, luego tenemos que calcular los valores de x para los cuales f(x)=0, habrá tantos como soluciones de la ecuación anterior.

-Cortes con el eje de ordenadas (OY): por tanto x=0, luego el punto de corte es (f(0),0).

3º) Regiones:

Una vez que hemos calculado los puntos de corte con el eje abscisas, podemos hallar cuál es el signo que tiene nuestra función. Para ello, haremos una tabla de dos filas, en la primera fila señalaremos los puntos de corte, así como los puntos que no están en el dominio; y en la segunda fila estudiamos el signo de la función en el intervalo correspondiente.

4º) Simetría:

Para facilitar el estudio de la función, ya que en el caso de ser simétrica podemos representarla en el intervalo (0, +∞) y después hacer su correspondiente simetría.

-Diremos que tiene simetría par cuando se cumpla f(x)=f(-x).

-Diremos que tiene simetría impar cuando se cumpla f(x)=-f(-x).

5º) Asíntotas:

Como ya se ha visto en otra ocasión, hay tres tipos de asíntotas:

–Asíntotas verticales: donde estudiamos el comportamiento de la función en los puntos que no están en el dominio.

–Asíntotas horizontales: en este caso estudiamos el comportamiento en el infinito.

–Asíntotas oblicuas: siempre y cuando no haya asíntotas horizontales.

Observación: Las funciones polinómicas no tienen asíntotas.

6º) Monotonía y extremos relativos:

Ya estamos casi finalizando… En penúltimo lugar tenemos que estudiar cuando crece y decrece la función, lo cual lo haremos por medio de la derivada: f´(x)=0.

Las soluciones de la ecuación anterior, son los posibles máximos o mínimos, como ya estudiamos en su momento, para recordarlo pinchad aquí, así como la curvatura de la función.

7º) Puntos de inflexión:

Un punto de inflexión es un punto en el que la función cambia su concavidad. Para encontrar estos puntos, necesitamos calcular la segunda derivada de la función y encontrar sus raíces. Es importante recordar que no todos los puntos en los que la segunda derivada es cero son puntos de inflexión. Para confirmar si un punto es de inflexión, debemos verificar que la función cambia su concavidad en ese punto.

8º) Periodicidad:

Si la función se repite a lo largo del eje x, diremos que es periódica. El periodo es la distancia entre dos repeticiones consecutivas de la función. Las funciones trigonométricas, como el seno y el coseno, son ejemplos comunes de funciones periódicas.

9º) Continuidad:

Una función es continua si no tiene saltos, huecos o asintotas. Para verificar la continuidad de una función, debemos comprobar que el límite de la función existe y es igual al valor de la función en todos los puntos de su dominio.

Ejemplo: Estudiar y representar la siguiente función: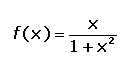

1º. Dominio: Como se trata de una función racional, igualamos el denominador a cero. Como en este caso no tiene solución real, entonces Dom f(x)=R.

2º. Puntos de corte:

Con el eje OX, igualamos f(x)=0→x=0→(0,0)

Con el eje OY, sustituyendo x=0, (0,0)

3º. Regiones:

4º. Simetría:

Tiene simetría par o respecto al origen ya que:

5º. Asíntotas:

-Asíntotas verticales: No tiene, ya que el dominio es todo R.

-Asíntota horizontal:

-Asíntota oblicua: Como tiene asíntota horizontal no tiene oblicua.

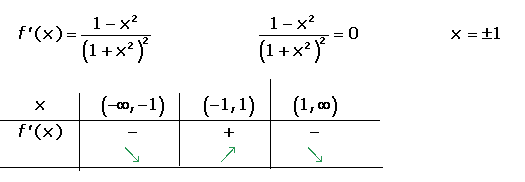
6º. Monotonía y extremos relativos:

Por tanto, tiene un mínimo en x=-1 y un máximo en x=1.

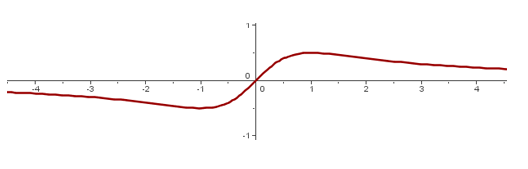
Recogemos los datos obtenidos en la siguiente gráfica: