Funciones racionales
Ya vimos hace unos días como representar las parábolas y sus características más significantes, ahora le ha llegado el turno a las funciones racionales.
Definición:Las funciones racionales son aquellas que se expresan mediante una fracción, donde tanto el numerador como el denominador son polinomios.
Concretamente, hoy veremos las funciones racionales formada por polinomios de primer grado, por tanto se puede expresar de la siguiente manera: ![]()
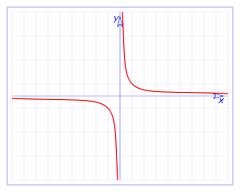
La representación de este tipo de funciones viene dada por medio de una hipérbola. Por tanto las características más representativas serán sus asíntotas: la vertical y la horizontal, como podemos ver en la siguiente imagen. Además, se define el centro de la hipérbola como el punto donde se cortan ambas asíntotas:
REPRESENTACIÓN DE y=k/x
Para representar las funciones racionales, comenzaremos viendo en primer lugar como representamos la función y=k/x.
1º. Estudiamos su dominio: Como se trata de una función racional, su dominio son todos los valores de x de la recta tales que no se anule el denominador, por tanto, todos los reales menos cuando x=0.
En este punto por tanto tendrá su asíntota vertical.
2º. Dependiendo del signo de k, tenemos que:
-si k>0, nuestra hipérbola se encuentra en el primer y tercer cuadrante, como la de la imagen anterior.
-si k<0, nuestra hipérbola se encuentra en el segundo y cuarto cuadrante.
El centro de la hipérbola es el (0,0)
TRANSFORMACIONES
A partir de la anterior: y= k/x, podemos representar todas las del tipo indicado arriba en la expresión (1) por medio de transformaciones que supondrán traslaciones en la hipérbola. Veremos las diferentes traslaciones y lo que ello conllevan:
-Traslación vertical: y=a+k/x
A partir de la hipérbola anterior, se produce un desplazamiento vertical de la hipérbola de a unidades, teniendo en cuenta que:
-si a>0, se traslada a unidades hacia arriba,
-si a<0, se traslada a unidades hacia abajo.
En este tipo de funciones racionales, diremos que en y=a hay una asíntota horizontal. Y el centro de la hipérbola es el (0,a)
-Traslación horizontal: y=k/(x+b)
En este caso, la hipérbola anterior se desplazará de forma horizontal, En este caso la asíntota vertical será x=-b. Para saber hacia donde se desplaza la hipérbola tenemos que tener en cuenta que:
-si b>0, se traslada b unidades hacia la izquierda,
-si b<0, se traslada b unidades hacia la derecha.
El centro de la hipérbola es (b,0)
-Traslación oblicua: y= a + k/(x+b)
Cuando aparecen de forma simultánea las dos traslaciones anteriores, nos encontramos con una traslación oblicua, que se traslada tanto de forma horizontal como vertical según el criterio antes descrito. En este caso el centro de la hipérbola será (b,a)
A continuación veremos un ejemplo de representación de funciones teniendo en cuenta lo que acabamos de ver:
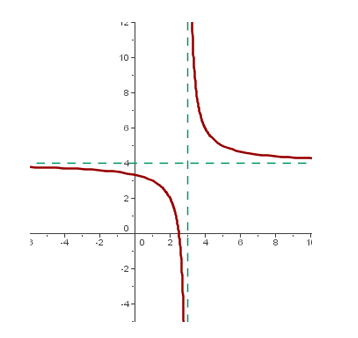
Ejemplo: Representa la función y= (4x-10)/(x-3)
1º.En primer lugar, tenemos que transformarla a la forma y=a+k/(x+b), para ello, realizamos la división de los polinomios, obteniendo, 4 de cociente y 2 de resto. Luego: y= 4+2/(x-3).
2º. Partimos de la función y=2/x, que sabemos que se representaría en los cuadrantes primero y tercero.
3º. Realizamos una traslación horizontal de 3 unidades hacia la derecha. La asíntota vertical es x=3.
4º. Realizamos una traslación vertical de 4 unidades hacia arriba. La asíntota horizontal es y=4.
5º. El centro de la hipérbola es el punto (3,4)
6º. La representación final es: