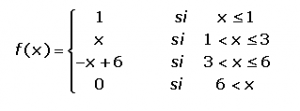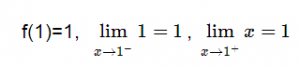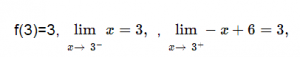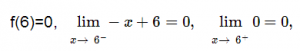Funciones a trozos

Como ya comentamos en el artículo de ayer, una función definida a trozos, es una función que consta de distintas expresiones algebraicas en cada uno de los intervalos ( o trozos) en los que está definida. Por tanto, para llevar a cabo el estudio de una función de este tipo, es necesario estudiar cada una de las funciones por separado en el intervalo en el que están definidas y luego estudiar el conjunto entero.

Vamos a centrarnos en dos aspectos fundamentales de este tipo de funciones. En primer lugar veremos cómo representarlas y a continuación estudiaremos la continuidad.

REPRESENTACIÓN DE UNA FUNCIÓN A TROZOS

Para llevar a cabo la representación de una función a trozos, en primer lugar estudiaremos cada uno de ellos, teniendo en cuenta si se tratan de rectas, parábolas, hipérbolas, una función constante, etc. Y dependiendo de cada caso, hallaremos los puntos necesarios. Recordemos que la función la tenemos que separar en el número de trozos como intervalos tenga la función, y que cada función no se puede salir de su intervalo.

Antes de realizar un ejemplo, recordaremos que cuando teníamos este símbolo ≤ o ≥, significaba que el último punto estaba incluido; pero cuando el símbolo era , el punto no formaba parte de la función y por tanto, pondremos un punto blanco.

Ejemplo: Realizar la representación de la siguiente función definida a trozos:

En este ejemplo tenemos cuatro funciones diferentes:

-Cuando x está en el intervalo (-∞,1], se trata de una función constante que vale 1.

-Cuando x está en el intervalo (1,3], tendremos que representar la recta y=x. Es muy importante dar en la tabla el valor de los extremos del intervalo, que pasa cuando x=1 y cuando x=3.

-Cuando x está entre (3, 6], es una recta; y=-x+6

-Cuando la x es mayor que 6, vuelve a tratarse de una función constante de valor 0.

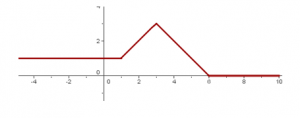
Por tanto obtenemos la siguiente representación:

CONTINUIDAD DE UNA FUNCIÓN

En primer lugar, es importante estudiar la continuidad de cada uno de los trozos en el intervalo en el que está definido. Después, pasamos a estudiar qué ocurre cuando se pasa de un trozo a otro de la función, para ello, recordamos la definición de continuidad en funciones definidas a trozos: para que una función sea continua en el punto x=a, tiene que coincidir el valor de la función en ese punto con el valor de los límites laterales.

Ejemplo: Estudiar la continuidad de la función anterior:

1º. El primer paso, como ya hemos mencionado es estudiar la continuidad de cada una de la funciones que forman mi función a trozos.

Cuando x está en el intervalo (-∞,1], es continua por tratarse de una función constante.

Cuando x está en el intervalo (1,3], es continua, ya que todas las funciones polinómicas son continuas en todo R.

Cuando x está entre (3, 6], es continua por la misma razón que la anterior.

Cuando la x es mayor que 6, es continua, al igual que en el primer intervalo.

2º. A continuación pasamos a estudiar qué ocurre en los extremos de los intervalos:

Cuando x=1. Es continua ya que:

-Cuando x=3. Es continua ya que:

-Cuando x=6. Es continua ya que: