Asíntotas verticales

Antes de empezar a ver que es una asíntota, es importante saber que en matemática algunas expresiones tales como “tender a “o aproximación indefinida” no se concretan claramente sino se utiliza terminantemente el concepto de límite. Este concepto hace referencia a la tendencia de una función a medida que los parámetros de esta se acercan a un valor determinado.

Una asíntota es una función que se representa gráficamente en forma de línea recta o parabólica. Cuando hablamos de líneas rectas, las asíntotas se aproximan continuamente a la función, cuando al menos una de las variables tanto X como Y tienden al infinito. Entonces cuando la curva se acerca a una recta, si X o Y tiende al infinito, llamamos a la recta, asíntota de la gráfica. Cuando no se acerca a ninguna recta se denomina Rama parabólica.

Una definición más formal sería la siguiente. Si un punto X o Y se mueve continuamente por una función Y=f (X) de modo que al menos una de sus coordenadas tenga tendencia al infinito, mientras que la distancia entre una recta determinada y dicho punto tienda a cero, se denominará a la recta asíntota de la función.

Las asíntotas se pueden clasificar como, asíntotas horizontales, asíntotas oblicuas o asíntotas verticales. Esta última será la que veremos detalladamente en este artículo.

Para calcular asíntotas verticales debemos tener en cuenta lo siguiente. En primer lugar calcular el dominio de la función dada. Luego de esto tomar el límite, para los valores de X a los cuales no pertenece al dominio. Entonces si el límite nos da infinito, podemos concluir en que tenemos una asíntota vertical.

Si queremos saber a que tiende una función, debemos tomar los límites laterales. La solución puede ser únicamente ± ∞. Las funciones que pueden poseer asíntotas verticales son las funciones racionales o las funciones logarítmicas o función tangente.

Asíntotas verticales (Paralelas al eje OY)

Si existe un número “a” tal, aplicamos la siguiente fórmula :

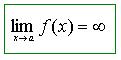
La recta “X = a” es la asíntota vertical

Veamos ahora un ejemplo:

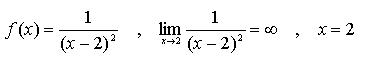
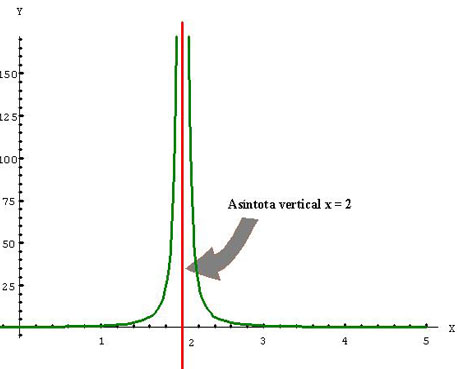
En la construcción de gráficas, las asíntotas verticales pertenecen a aquellos valores de la variable independiente que indefinen a las funciones como divisiones entre cero.No hay limitaciones en cuanto al número de asíntotas verticales que puede tener una función.