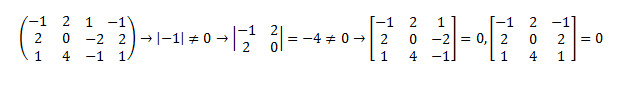Rango de una matriz
Ya hemos trabajado en numerosas ocasiones con matrices y de hecho, también hemos hablado del rango de una matriz; ¿pero a qué nos referimos con rango de una matriz? ¿Y cómo podemos calcularlo? Estas son las preguntas a las que vamos a dar respuesta en este post. Además, profundizaremos en las aplicaciones y la importancia del rango de una matriz en distintos campos de la matemática y la física.
Comenzaremos en primer lugar dando la definición, y a continuación veremos dos métodos para hallar el rango de una matriz: el método de Gauss y orlando por determinantes.
DEFINICION
El rango de una matriz es el número de filas o columnas linealmente independientes. Es decir, si consideramos cada fila o columna de una matriz como vectores, el rango de la matriz es el número de vectores linealmente independientes, y que por tanto pertenecerían a la base del espacio.
MÉTODOS PARA CALCULAR EL RANGO
-Método de Gauss
Este método consiste en hacer ceros en la matriz por debajo de la diagonal principal mediante operaciones con las filas (no obstante también podrían realizarse operaciones con las columnas). El rango será el número de filas distintas de cero que nos queden.
Ejemplo: Como podemos observar en el siguiente ejemplo, en primer lugar hacemos ceros en la primera columna utilizando la primera fila, quedando ésta fija. Una vez que ya hemos hecho ceros en la primera columna pasamos a hacer ceros en la segunda columna, utilizando la segunda fila y dejando fija la primera fila y la segunda.
Nuestra matriz tiene orden dos, ya que quedan dos filas distintas de cero.
– Orlar menores
El método de orlar menores, consiste en comenzar buscando un menor de orden dos cuyo determinante sea distinto de cero, y a continuación orlar, es decir añadir una fila y una columna a este determinante, para nuevamente calcularlo y obtener un determinante que sea distinto de cero. El rango de la matriz será el orden del mayor menor con determinante distinto de cero que se obtenga.
Ejemplo: Vamos a realizar el mismo ejemplo utilizando el método de orlar menores.
Como podemos observar a continuación, en primer lugar elegimos cualquier número distinto de cero, por ejemplo el término a11, ya que |-1|≠0. A continuación, buscamos un determinante de orden dos que nos de distinto de cero, obtenido a añadir a -1 una fila y una columna, por ejemplo los cuatro primeros números.
Por último, orlamos estos cuatro número añadiendo una fila y una columna, si el determinante obtenido nos da cero volvemos a orlar con otra fila distinta. Como este determinante también nos da cero y ya no tenemos más filas para orlar, entonces el rango de la matriz será 2.
APLICACIONES DEL RANGO DE UNA MATRIZ
Entre las aplicaciones más destacas del rango de una matriz se encuentran:
– La discusión y resolución de sistemas de ecuaciones lineales: cuando la matriz de los coeficientes y la matriz ampliada tienen el mismo rango el sistema tiene solución.
– Para determinar la linealidad de los vectores de una base.
– Para determinar la dimensión del núcleo de una aplicación lineal: dim (Ker f)
– En la teoría de control se utilizan para determinar si un sistema es controlable u observable.
Además de estas aplicaciones, el rango de una matriz también tiene un papel importante en la teoría de la codificación y la criptografía. En la codificación, el rango de una matriz se utiliza para determinar la eficiencia de un código, mientras que en la criptografía, se utiliza para determinar la seguridad de un sistema criptográfico.
Por otro lado, el rango de una matriz también tiene aplicaciones en la física, particularmente en la teoría de la relatividad y la mecánica cuántica. En la teoría de la relatividad, el rango de una matriz se utiliza para determinar la dimensionalidad del espacio-tiempo, mientras que en la mecánica cuántica, se utiliza para determinar la independencia de los estados cuánticos.
En resumen, el rango de una matriz es una herramienta matemática fundamental que tiene aplicaciones en una amplia variedad de campos. Por lo tanto, es esencial entender cómo calcularlo y cómo interpretarlo correctamente.