Inversa de una matriz
Una matriz es una tabla rectangular de datos o números, denominados elementos o entradas de matriz, que se ordenan en filas y columnas. Las filas representan las líneas horizontales de la matriz y las columnas las líneas verticales. Pueden sumarse, multiplicarse o descomponerse de diversas formas, lo que las hace importantes en el campo del algebra lineal, que se encarga de estudiar vectores, matrices, sistemas de ecuaciones lineales, espacios vectoriales y transformaciones lineales. Aparecen en forma natural en geometría, estadística, economía, física, etc.
Se llama entonces matriz de orden m x n a un conjunto rectangular de elementos que se disponen en m filas y en n columnas. Se denomina dimensión o tamaño al orden de una matriz, siendo m y n números naturales.
Las matrices se indican con letras mayúsculas y sus elementos con letras minúsculas y subíndices que demuestran el lugar ocupado. Un elemento genérico que ocupara la fila i y la columna j se escribirá aij. Si el dicho elemento apareciera entre paréntesis también representaría a toda la matriz con la siguiente forma, A =(aij) Veamos un ejemplo:

Si hacemos referencia a filas o columnas estamos hablando de líneas. Entonces el número total de elementos de una matriz es Am x n o sea m.n. Tanto las listas como las tablas adoptan el nombre genérico de matrices.
Sabiendo esto, veamos a continuación que es la inversa de una matriz.
Dada una matriz cuadrada A, si existe otra matriz B del mismo orden que compruebe que:
A.B= B.A=I ( I es igual a la matriz identidad) diremos que B es la matriz inversa de Z y se representa de la siguiente forma:
![]()
Si hay una matriz inversa de A, diremos que dicha matriz es inversible o regular. Si esto no se cumple diremos que la matriz A es singular. Una matriz tiene inversa por ejemplo si una matriz A de orden n (es decir de n filas y n columnas) tiene inversa si el rango es n, o sea cuando el rango de la matriz coincide con su orden.
Existen tres procedimientos para calcular la inversa de una matriz. Uno de ellos es por el método de Gauss. El otro por determinantes y adjuntos y también aplicando la definición y resolviendo los sistemas de ecuaciones que corresponda.
El método de Gauss, también conocido como eliminación gaussiana, es un procedimiento sistemático para resolver sistemas de ecuaciones lineales. Este método transforma la matriz original en una matriz identidad mediante una serie de operaciones elementales de fila, y simultáneamente aplica estas operaciones a una matriz identidad para obtener la inversa.
El método de determinantes y adjuntos implica calcular el determinante de la matriz original y luego usar los cofactores para formar la matriz adjunta. La inversa se obtiene dividiendo la matriz adjunta por el determinante de la matriz original. Este método es más práctico para matrices de menor tamaño debido a la complejidad del cálculo de determinantes para matrices grandes.
El tercer método, que utiliza la definición de matriz inversa, se basa en resolver un sistema de ecuaciones lineales. Para una matriz A de orden n, se resuelven n sistemas de ecuaciones lineales, uno para cada columna de la matriz identidad, para encontrar las columnas correspondientes de la matriz inversa.
Veamos por último, un ejemplo de matriz inversa.
Aquí diremos que una matriz cuadrada A tienen inversa A-1, si verificamos que:
![]()
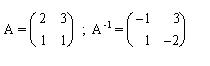
Es importante destacar que no todas las matrices cuadradas tienen inversa. Las matrices que no tienen inversa se denominan matrices singulares. Una matriz es singular si su determinante es cero. En términos prácticos, esto significa que una matriz singular no puede ser invertida porque no tiene una única solución para el sistema de ecuaciones lineales asociado.
Además, la inversa de una matriz tiene aplicaciones significativas en diversas áreas. Por ejemplo, en la resolución de sistemas de ecuaciones lineales, la matriz inversa se utiliza para encontrar soluciones exactas. En el campo de la informática, las matrices inversas son esenciales en algoritmos de gráficos y procesamiento de imágenes. En economía, se utilizan para modelar y resolver problemas de optimización.
Finalmente, es relevante mencionar que el cálculo de la inversa de una matriz puede ser computacionalmente intensivo, especialmente para matrices de gran tamaño. Por esta razón, en aplicaciones prácticas, a menudo se utilizan métodos numéricos y software especializado para encontrar la inversa de matrices grandes.
