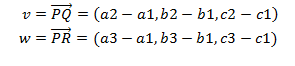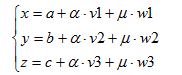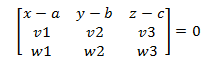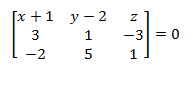Ecuaciones del plano

Como lo prometido es deuda, en este post veremos las diferentes formas en las que podemos encontrarnos la ecuación de un plano en el espacio tridimensional.

Un plano queda determinado por :

-Un punto (P) y dos vectores (v,w): P(a,b,c), v=(v1,v2,v3) y w=(w1,w2,w3)

-O tres puntos: P(a1,b1,c1), Q(a2,b2,c2) y R(a3,b3,c3), de los cuales para escribir la ecuación del plano, elegiríamos uno de ellos, y formaríamos dos vectores con los otros dos (para lo cual es necesario que P, Q y R no estén alineados).

Suponiendo que nos dan un punto P y dos vectores v y w, seguiremos el orden que utilizamos en las ecuaciones de la recta.

En primer lugar tenemos la ecuación vectorial:

(x,y,z)=(a,b,c) +α (v1,v2,v3)+µ(w1,w2,w3)

Igualando componente a componente, obtenemos las ecuaciones paramétricas del plano:

Continuando con el paralelismo existente con las ecuaciones de la recta en el espacio, tendríamos que despejar el parámetro. En este caso, vamos a resolver este sistema donde nuestras incógnitas son α y µ. Para ello, transformamos el sistema anterior en este otro:

Dejando las incógnitos a la derecha del sistema. Para que este sistema tenga solución es necesario y suficiente que el rango de la matriz ampliada sea dos (es evidente que el rango de la matriz de los coeficientes es dos ya que se tratan de dos vectores linealmente independientes). Por tanto, si el rango de la matriz ampliado tiene que ser dos, su determinante será igual a cero. Obteniendo la ecuación en forma de determinante:

Si resolvemos el determinante y llamamos A, B y C a los coeficientes de x, y, z respectivamente y D al término independiente obtenemos la ecuación general, cartesiana o ímplicita. (En efecto la podemos llamar de cualquiera de las siguientes maneras, que es la misma)

Ax+By+Cz+D=0

Esta ecuación del plano, nos permite obtener un vector normal del plano n=(A,B,C) . Este vector es por tanto, el vector director de la recta perpendicular al plano.

Esta última forma de dar la ecuación de un plano es la que normalmente utilizamos cuando queremos estudiar la posición relativa de tres planos en el espacio.

Para finalizar, y poder visualizar de forma más sencilla todo lo explicado realizaremos un ejemplo:

Ejemplo: Dados el punto P(-1,2,0) , y los vectores v=(3,1,-3) y w=(-2,5,1) escribir las ecuaciones del plano de todas formas posibles.

Vamos a seguir los mismos pasos que hemos mencionado de forma teórica.

En primer lugar escribimos la ecuación vectorial del plano:

(x,y,z)=(-1,2,0) + α(3,1,-3) + µ(-2,-5,1)

Separando por coordenadas obtenemos las ecuaciones paramétricas:

Dejando a la derecha nuestras incógnitas α y µ, obtenemos el siguiente sistema.

Y escribiendo el determinante de la matriz ampliada igualada a cero, obtenemos la ecuación del plano en forma de determinante:

Resolviendo el determinante obtenemos, por último, la ecuación implícita del plano:

16x+3y+17z+9=0

De la que obtenemos el vector normal del plano n=(16,3,17).

Otra forma de calcular el vector normal es haciendo el producto vectorial de los vectores v y w.

n = vxw