Determinantes de orden

Antes de adentrarnos en el tema de las determinantes, recordemos el concepto de matriz. Una matriz es un conjunto de elementos de cualquier naturaleza, generalmente suelen ser números establecidos en filas y columnas. Se denomina matriz de orden «m × n» a un conjunto cuadrangular de componentes ordenados en m filas y en n columnas. El orden de una matriz se denomina también dimensión o tamaño, siendo m y n números naturales.

El determinante es una función que le otorga a una matriz de orden n, un único número real denominado determinante de la matriz. Entonces si A es una matriz de orden n, el determinante de la matriz A lo indicaremos como det (A) o puede ser también │A│ las barras no simbolizan valor absoluto.

Para el cálculo de determinantes de matrices de cualquier orden, existe una regla la cual (teorema de Laplace) reduce el cálculo a sumas y restas de varios determinantes de un orden inferior. Este proceso se puede repetir tantas veces como sea necesario hasta reducir el problema al cálculo de múltiples determinantes de orden tan pequeño como se quiera. Sabiendo que el determinante de un escalar es el propio escalar, Es posible calcular el determinante de cualquier matriz aplicando dicho teorema.

La definición de una determinante de matriz de orden 1, Si A= [a] es entonces det(A)=a

Veamos un ejemplo que nos dejará mas claro esto:

En el caso de matrices de orden dos o tres (que sería de orden inferior) utilizaremos sencillas reglas, provenientes del teorema de laplace. Veamos como serían los determinantes de una matriz de orden dos:

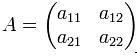
Lo calcularemos con la siguiente fórmula:

Un determinante de orden tres se puede calcular utilizando la regla de Sarrus. Esta regla se aplica solo a los determinantes de tercer orden. Veamos un ejemplo tomando una matriz 3×3:

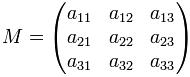
Para calcular esto, debemos repetir las dos primeras columnas de la matriz a la derecha de modo que queden cinco columnas en fila. Luego sumamos los productos de las diagonales descendentes que están en linea continua y por último restamos los productos de las diagonales ascendenteso en trozos. El resultado será el siguiente:

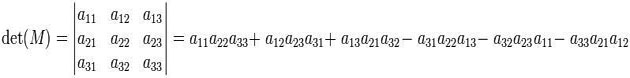
En caso de tener un determinante de orden 4, se conseguirán directamente determinantes de orden 3 que lograrán ser calculados por la regla de Sarrus. Pero en los determinantes de orden superior, como es el caso de n = 5, ocurre que al desarrollar los componentes de una línea, adquirimos determinantes de orden 4, que a la vez se deberán desarrollar por el mismo procedimiento, para obtener de este modo determinantes de tercer orden. Si queremos obtener con el método descrito un determinante de orden 4, debemos calcular entonces 4 determinantes de orden 3. De otro modo, si anteriormente se obtienen tres ceros en una fila o columna, bastara con calcular solamente un determinante de orden 3, Puesto que el resto de lo determinantes quedarán multiplicados por 0, por lo cual quedarán anulados

En un determinante de orden 5, obtendremos 5 determinantes de orden 4 a desarrollar y que nos dará como resultado 20 determinantes de orden 3. Por lo tanto el número de determinantes de tercer orden que se adquieren en el desarrollo de un determinante de orden n es n/3.