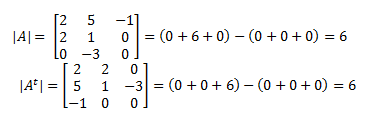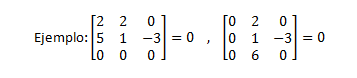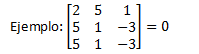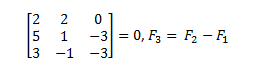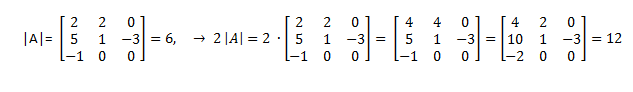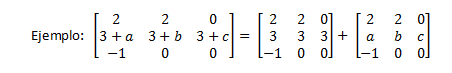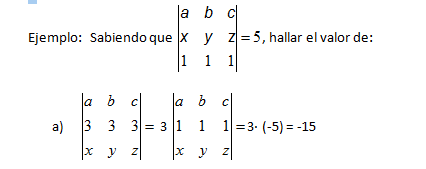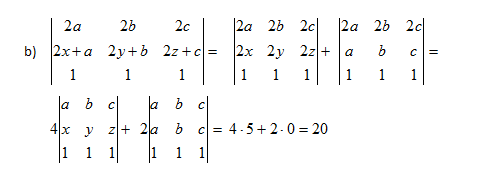Propiedades de los determinantes

Una vez que ya conocemos a fondo las matrices, podemos centrarnos en el estudio de los determinantes.

Como ya se vio en otra ocasión la definición de determinante, hoy veremos cuales son sus propiedades y algunos ejemplos:

1. El determinante de una matriz y el de su traspuesta son iguales:

Ejemplo: Calculamos el determinante de A y de su traspuesta mediante la regla de Sarrus.

2. Si la matriz tiene una fila o una columna en la que todos sus elementos son cero, entonces |A|=0.

3. Si la matriz tiene dos filas o dos columnas iguales, entonces su determinante también es cero: |A|=0.

4. Si la matriz tiene una fila o columna que sea combinación lineal de alguna de las otras, entonces |A|=0.

Ejemplo: En el siguiente determinante, la última fila es el resultado de restarle a la segunda fila la primera.

5. El determinante de una matriz triangular, (tanto si es superior como inferior) se obtiene multiplicando los elementos de la diagonal principal.

6. Si intercambiamos el orden de dos filas, el determinante cambia de signo.

7. Si multiplicamos un determinante por un número real, quedará multiplicado por ese número únicamente una fila o una columna:

Ejemplo: Si hacemos el determinante de la matriz A y lo multiplicamos por 2, se obtiene lo mismo que el determinante de la matriz A en la que hemos multiplicado la primera fila por 2, o la primera columna, (podríamos multiplicar cualquiera de las filas o las columnas, pero sólo una)

8. Si en un determinante una fila o una columna está formada por dos sumandos, el determinante se descomponen en la suma de dos determinantes, uno con el primer sumando y el otro con el segundo sumando:

9. El determinante de la suma de dos matrices es igual a la suma de los determinantes: |A+B|=|A|+|B|

10. De forma análoga a la anterior, el determinante del producto de dos matrices, es igual al producto de los determinantes: |A•B|=|A|•|B|

11. El determinante de un número real por una matriz es igual al número real elevado al número de filas, por el determinante de la matriz. Esta propiedad se deriva de la propiedad 7. |αA|= α^n∙|A|, donde n es el número de filas de la matriz A.

Para finalizar con las propiedades de los determinantes, vamos a realizar un ejercicio típico de aplicación de algunas de las propiedades que acabamos de ver.

En primer lugar hemos aplicado la propiedad 7, como el tres está multiplicando a la segunda fila lo podemos poner delante multiplicando a todo el determinante. Y por último hemos aplicado la propiedad 6, como están intercambiadas la última fila y la segunda, cambiamos el signo del determinante.

En primer lugar utilizamos la propiedad 8 y separamos los sumandos de la fila 2 en dos determinantes. En el primer determinante como tanto la primera como la segunda fila están multiplicadas por 2, por la propiedad 7, el determinante queda multiplicado por 2 al cuadrado. En el segundo determinante, por la propiedad 7 otra vez, como la primera fila está multiplicada por dos, el determinante queda multiplicado por dos. Por último, por la propiedad 3, como tenemos dos filas iguales el determinante vale 0.