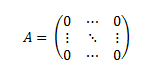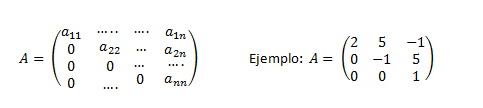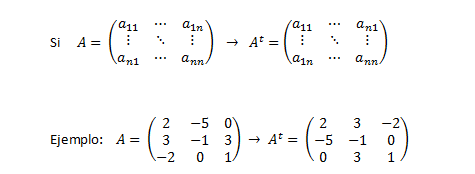Tipos de matrices

Una vez vista la definición de matriz y antes de estudiar las distintas operaciones que se pueden realizar en el conjunto de las matrices, vamos a ver los distintos tipos que hay, así como las propiedades más importantes.

Matriz fila: Es la matriz que únicamente tiene una fila, por tanto es de orden 1xn:

Ejemplo: A = ( 1 3 – 5 7 ), que es de orden 1×4

Matriz columna: De forma análoga a la anterior esta matriz consta sólo de una columna, será de orden n x 1:

Matriz cuadrada: Es una matriz que tiene el mismo número filas que de columnas, y por tanto será de orden nxn. Los elementos aii se denominan diagonal principal.

Matriz nula: Es una matriz cuadrada en la que todos sus elementos son cero.

Matriz triangular superior: Es una matriz cuadrada en la que todos los elementos que hay por debajo de la diagonal principal son ceros:

Matriz triangular inferior: Es el caso contrario al anterior, es decir, una matriz cuadrada en la que todos los elementos por encima de la diagonal principal son ceros.

Matriz diagonal: Es una matriz cuadrada que tiene todos los elementos nulos excepto los de la diagonal principal.

Matriz identidad: Es una matriz diagonal, en la que todos los elementos son 1.

Matriz traspuesta: Es la matriz que se obtiene al intercambiar filas por columnas de una matriz dada, no es necesario que sea una matriz cuadrada.

Propiedades de la matriz traspuesta:

1. La matriz traspuesta de una matriz traspuesta, es la matriz inicial:

2. La traspuesta de la suma de matrices, es la suma de sus traspuestas:

3. La traspuesta de un número por una matriz, es igual al número por la traspuesta de la matriz:

4. La traspuesta del producto de dos matrices, es el producto de las matrices traspuestas invirtiendo el orden de los factores. (El producto de matrices no es conmutativo)

Matriz regular: Es una matriz cuadrada que tiene inversa, además el determinante de una matriz regular siempre es distinto de cero.

Matriz singular: El caso contrario del anterior, cuando la matriz no tiene inversa, se denomina matriz singular, y por tanto el determinante de una matriz singular siempre es igual a cero.

Matriz Idempotente: Es una matriz que al multiplicarla por ella misma (es decir, al elevarla al cuadrado) se obtiene la mima matriz:

Matriz involutiva: Es una matriz que al multiplicarla por ella misma se obtiene la matriz identidad:

Matriz simétrica: Es una matriz cuadrada que al hacerle la traspuesta da ella misma:

Matriz antisimétrica o hemisimétrica: Es una matriz cuadrada cuya traspuesta es ella misma a excepción de que todos los elementos que la forman tienen signos contrarios:

Matriz ortogonal: Es aquella matriz que verifica que si la multiplicamos por su traspuesta, obtenemos la matriz identidad: