Sistema de 3 ecuaciones
Un sistema de ecuaciones lineales o sistema lineal, se trata de un conjunto de ecuaciones lineales sobre una estructura algebraica que llamamos cuerpo. Esta estructura permite que las operaciones de suma, y multiplicación se puedan llevar a cabo cumpliendo también con las propiedades asociativa, distributiva y conmutativa, aparte de la existencia de su inverso a la suma y la multiplicación, lo cual permite que se efectúen restas y divisiones. Veamos ahora un ejemplo de sistema lineal de ecuaciones:
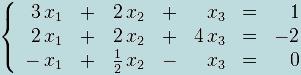
El problema de esto radica en hallar los valores desconocidos de las variables, x1, x2 y x3 pertenecientes a las tres ecuaciones que podemos observar.
Es importante saber que a los tradicionales sistemas de dos ecuaciones y dos incógnitas podemos agregar las ecuaciones que queramos para obtener de esta forma sistemas de 3, 4 o incluso mas ecuaciones. Pero al aumentar el número de ecuaciones se vuelve mas confuso y difícil solucionarlo con los clásicos métodos como la reducción, igualación o sustitución, por lo cual es conveniente aplicar el método de Gauss, que también se utiliza para resolver sistemas de ecuaciones. De todos modos no explicaremos este método por el momento y esperaremos al siguiente artículo en el cual lo veremos detalladamente.
Dado un sistema de tres ecuaciones con tres incógnitas, estarán asociadas dos matrices, una será A, o sea la matriz de coeficientes y la otra A* la matriz ampliada. Se le agrega a la matriz de coeficientes la columna de los términos independientes.
Para resolver este tipo de ecuaciones hay varios métodos. Entre ellos el ya nombrado método de Gauss, y la regla de Cramer. Más adelante explicaremos cada uno de estos métodos que nos ayudarán a resolver sistemas de tres ecuaciones y tres incógnitas.
Para la interpretación geométrica de los sistemas con tres ecuaciones y tres incógnitas, debemos tener en cuenta lo siguiente. Como cada ecuación lineal con tres incógnitas pertenece a un plano en el espacio, el resultado corresponderá a la posición en la cual los planos estén en el espacio. Lo más simple es conocer que pasa con los planos dos a dos, ya que en el espacio dos planos pueden estar solamente en tres posiciones.
Si están en la posición coincidente, nos daremos cuenta ya que sus correspondientes ecuaciones tendrán los coeficientes de las incógnitas y sus términos independientes en proporción o sea que los planos serían estos:
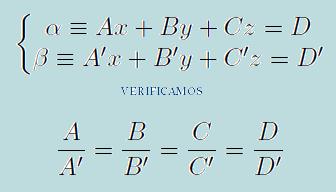
Aquí por ejemplo los planos 2x+3y-z=5, y -10x-15y+5z=-15. Por lo cual son coincidentes.
La otra posición en la cual pueden encontrarse los planos, es la posición paralela. En este caso los coeficientes de las incógnitas serán proporcionales, pero sus términos no. Por lo cual:
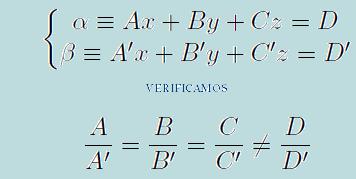
Por ejemplo los planos 2x+3y-5 y -10x-15y+5z= 7
En el último caso diremos que son secantes cuando los coeficientes no son proporcionales. De modo que:
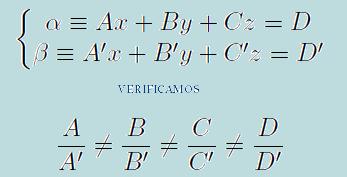
Por ejemplo los planos 7x+3y-z=5 y 10x-15y+5z=7
Los tres casos son posibles, siempre que se puedan realizar las divisiones
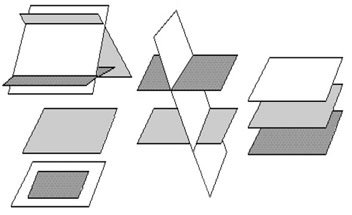
Ya que podemos determinar la posición de los planos 2 a 2, podemos determinar también en que posición se hallan los 3 a la vez, puntualizándonos en los casos siguientes:
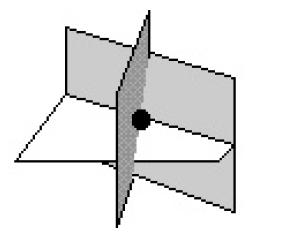
Si el sistema tiene una solución única, en la cual los tres planos se cortan en un punto, que corresponde a la solución del sistema tendremos lo que se muestra continuación:
Si el sistema tiene soluciones infinitas puede ocurrir que los tres planos se corten en una recta. que dos sean coincidentes y que el restante se corte en una recta o que los tres sean coincidentes. Observemos:
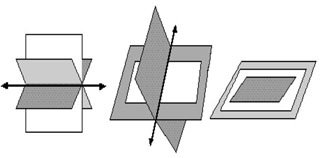
Por último si el sistema no tiene solución puede suceder que los planos se corten de a dos. Que los tres planos sean paralelos. Que dos sean paralelos y el restante los corta. Que se encuentren dos planos paralelos y el restante sea coincidente con uno de ellos. Observemos la representación de esto: