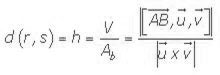Distancias en el plano

La distancia es una forma de expresar tanto la lejanía como la proximidad entre dos cuerpos o así mismo el intervalo de tiempo que sucede entre dos casos. Podemos decir que las subvariedades lineales del plano son las rectas y los puntos. Entonces si hablamos de distancias entre variedades lineales en el plano nos podemos referir a la distancia entre dos puntos, la distancia entre una recta y un punto o la distancia entre dos rectas.

La distancia entre dos puntos se establece dados dos puntos del plano. Cuando los puntos están ubicados sobre el eje x o en una recta que sea paralela a ese eje, la distancia entre los puntos pertenece al valor absoluto de la diferencia de sus abscisas. Pongamos como ejemplo la distancia entre los puntos (-4,0) y (5,0) que es 4+5=9 unidades. Si los puntos están ubicados sobre el eje y/o en una recta paralela a dicho eje, la distancia entre los puntos será correspondiente al valor absoluto de la diferencia de sus ordenadas. Pero si los puntos se hallan en un lugar cualquiera del sistema de coordenadas queda determinada por la fórmula que mostraremos a continuación, pero antes de esto tomemos como ejemplo lo siguiente:

A=(a1,b1) y B=(a2,b2) aquí se determina la distancia entre dos puntos a través de la dicha fórmula.

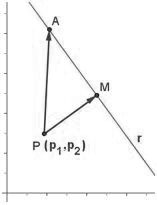
Para encontrar la distancia entre una recta y un punto es la longitud del segmento perpendicular a la recta, la cual está trazada desde el punto diremos que dada una recta r:Ax+By+C=0 y P=(p1,p2) un punto que no está contenido en ella. La distancia entre el punto y la recta será dada por la siguiente fórmula:

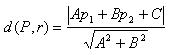
Observemos un ejemplo:

En caso de querer hallar la distancia entre dos rectas debemos tener en cuenta que si dos rectas en el plano no son paralelas se cortarán en un punto y por lo tanto la distancia entre las dos será 0. Por esto solo tiene sentido estudiar la distancia entre dos rectas únicamente si son paralelas. O sea que r:Ax+By+C=0 y s:A»x+B»y+C»=0 son dos rectas paralelas. Entonces para hallar la distancia entre ambas debemos tomar un punto de una de ellas como por ejemplo de r y se calcula de esta forma la distancia de ese punto a s.

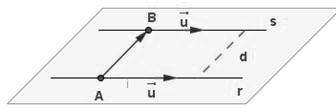
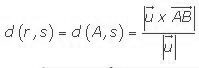
Podemos medir la distancia entre dos rectas que se cruzan si las medimos sobre una perpendicular común. Siendo los vectores las de terminaciones lineales de las rectas correspondientes a r y s.

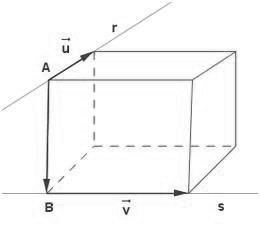
Entonces los vectores Ab, u y v determinan el paralelismo con el poliedro que se muestra, cuya altura es la distancia entre las dos rectas. El volumen de un paralelepípedo o sea un poliedro de seis caras es:

Si tenemos en cuenta que el volumen es el valor absoluto del producto resultante mixto de los tres vectores y que el área de la base corresponde al producto vectorial de los vectores que son los directores de las rectas, la distancia o altura entre los dos puntos será lo mismo que: