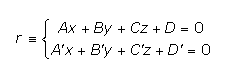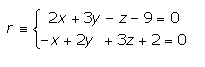Haz de planos

Volvemos de nuevo a los conceptos geométricos, donde resaltaremos en este caso la posición relativa de dos planos. Ya hablamos unos días atrás del haz de rectas, hoy es la ocasión de hablar del haz de planos. Al igual que en el caso de las rectas, estudiaremos el haz de planos paralelos y por otro lado el haz de planos que pasan por una recta.

HAZ DE PLANOS PARALELOS

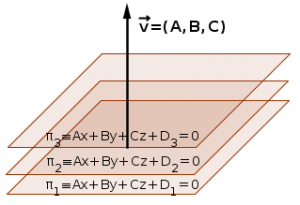Si en la expresión de un plano cualquiera π: Ax+By+Cz+D=0 se fijan los coeficientes de A, B y C dejando variar D, la nueva expresión Ax+By+Cz+D»=0 representa un conjunto de planos denominado haz de planos paralelos.

Observación: Para determinar el plano del haz que pasa por un punto dado P(x0,y0,z0), hay que sustituir las coordenadas del punto en la ecuación del haz, y hallar el punto D» que satisfaga la ecuación. Sustituyendo en la ecuación del haz por el D» correspondiente se obtiene el plano pedido.

Ejemplo: a) Hallar la ecuación del haz de planos paralelos al plano π: 3x-y+z-3=0.

b) Hallar el plano perteneciente al haz anterior que pasa por el punto P(1,2,1).

a) El haz de de planos paralelos al plano dado es 3x-y+z+D»=0.

b) Sustituyendo en la ecuación del haz el punto dado obtenemos el valor de D»: 3∙1-2+1+D»=0 → D»= -2. Por tanto la ecuación del plano del haz que pasa por el punto P es: π»: 3x-y+z-2=0.

HAZ DE PLANOS QUE PASAN POR UNA RECTA

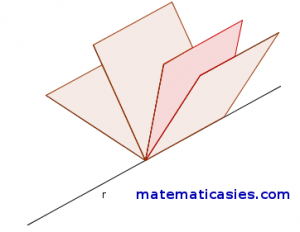Llamamos haz de planos de arista una recta r dada, al conjunto de los planos que contienen a dicha recta r. Es decir, es la recta donde cortan los planos como podemos ver en la siguiente imagen.

Supongamos que una recta viene dada por su ecuación implícita:

Hemos visto que para un plano π: A»»x+B»»y+C»»z+D»»=0 contenga a la recta r debe cumplirse que el rango de la matriz formada por las filas (A,B,C), (A»,B»,C») (A»»,B»»,C»») tiene que coincidir con el rango de la matriz ampliada, formada por las filas (A,B,C,D), (A»,B»C»,D») y la fila (A»»,B»»,C»»,D»»), este rango es 2. Por tanto, (A»»,B»»,C»»,D»») es combinación lineal de los otros dos vectores. De esta manera obtenemos el haz de planos de arista la recta r: (Ax+By+Cz+D)+λ(A»x+B»y+C»z+D»)=0, con λ una constante real no nula.

Ejemplo: a) Halla la ecuación del haz de planos que contiene a la recta

b) Hallar la ecuación del plano correspondiente al haz anterior que pasa por el punto P(3,2,-3).

a) La ecuación del haz es: (2x+3y-z-9)+ λ(-x+2y+3z+2)=0.

b) Sustituyendo el punto en la ecuación del haz el punto, obtenemos que λ=1. Sustituyendo este valor en la ecuación del haz obtenemos el plano pedido: π: 2x+3y-z-9-x+2y+3z+2=0 → π: x+5y+2z-7=0.