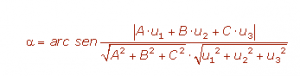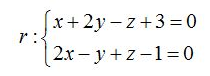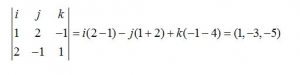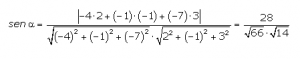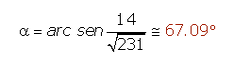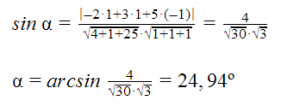Ángulo entre una recta y un plano
Hoy vamos a estudiar como calcular el ángulo que forma una recta y un plano.
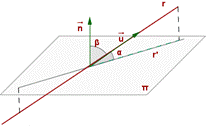
Para poder calcular el ángulo que forman, calcularemos el ángulo que forma la recta con su proyección ortogonal sobre el plano. Es decir, para calcular el ángulo que forman, nos valdremos del vector normal del plano y del director de la recta, de tal forma que el ángulo buscado será el complementario del que forman estos dos vectores, como podemos apreciar en la siguiente imagen.
Por tanto, utilizando la fórmula del ángulo formado por dos rectas, y sabiendo que por ser ángulos complementarios se cumple que sen α = cos (90º-α).
Dada la ecuación del plano en forma implícita, π: Ax+By+Cz+D=0 y la ecuación de la recta r determinada por un punto y un vector: r:{P, v}, entonces, como ya hemos comentado, utilizaremos el ángulo que forman el vector normal al plano n=(A,B,C) y el vector director del plano v=(u1,u2,u3):
Observación: Recordad que en primer lugar debemos comprobar la posición relativa del plano y la recta, ya que puede ocurrir que sean coincidentes o paralelos y por tanto no determinan ningún ángulo, en este caso, el vector normal y el director de la recta son proporcionales, de tal forma que se cumple u1/A=u2/B=u3/C.
Ejemplo 1: Hallar el ángulo que forma el plano π: -x-y-2z-5=0 y la recta de ecuación:
En primer lugar, como la ecuación viene dada de forma implícita tenemos que calcular el vector director de la recta. Para ello realizamos el siguiente producto vectorial:
Luego el vector director de la recta es v=(1,-3,-5), y el vector normal del plano es n=(-1,-1,-2). Como los vectores no son proporcionales, la recta y el plano se cortan, por tanto sustituyendo en la fórmula anterior obtendremos el ángulo que forman:
Por último, para hallar el ángulo, tenemos que hacer la inversa del seno, por tanto, haciendo el arcoseno:
Por tanto, el ángulo que forma la recta r y el plano π es aproximadamente 67º.
Ejemplo 2: Halla el ángulo formado por el plano determinado por el punto A(1,1,1) y tiene como vectores directores v=(1,-1,1) y u=(2,3,-1), y la recta determinado por el punto B(0,1,-2) y el vector w=(2,1,-1).
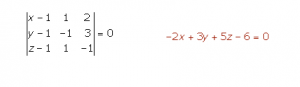
En primer lugar hallamos la ecuación implícita o general del plano, y de esta manera tendremos el vector normal. O también podemos realizar el producto vectorial del vector v y u para obtener el vector normal del plano:
Luego el vector normal del plano es n=(-2,3,5).
Como ya tenemos el vector director de la recta w=(2,1,-1), podemos comprobar que los vectores no son proporcionales y por tanto se cortan. Para calcular el ángulo que forman utilizamos la fórmula dada anteriormente:
Por tanto, el ángulo que forman la recta y el plano es aproximadamente 25º.
Una vez visto estos ejemplos en los que la única dificultad es hallar los vectores de los planos que necesitamos, estamos preparados para calcular el ángulo que forman un plano y una recta en cualquier situación.