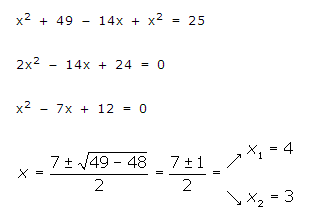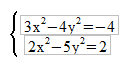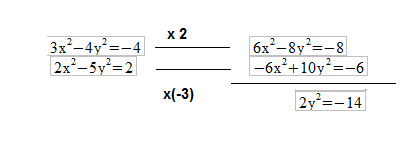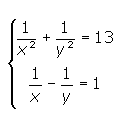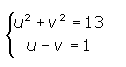Sistema de ecuaciones no lineales

Una vez que ya hemos visto los métodos que existen para poder resolver sistemas de ecuaciones lineales, vamos a estudiar también cómo resolver algunos de los sistemas no lineales empleando estos métodos. Es muy importante elegir el método adecuado, ya que en caso contrario su resolución podría ser muy pesada, difícil y por tanto con facilidad de cometer errores.

Llamamos sistema no lineal a un sistema de ecuaciones en el que una o ambas de las ecuaciones que forman el sistema es una ecuación no lineal, es decir, cuando alguna de las incógnitas que forman parte de la ecuación no son de primer grado. Por tanto en este tipo de sistemas nos podemos encontrar polinomios de segundo grado, raíces, logaritmos, exponenciales….

La mayor parte de estos sistemas se resuelven utilizando el método de sustitución, aunque en algunos casos puede ocurrir que no sea la forma más sencilla. A continuación veremos algunos de estas excepciones a través de ejemplos. Podemos distinguir por tanto algunos casos:

CASO 1: Si una de las ecuaciones es lineal y la otra no lineal:

En este caso utilizaremos siempre el método de sustitución:

Como podemos observar, en este caso la segunda ecuación es una ecuación lineal, por tanto seguiremos los pasos que vimos en el método de sustitución:

1º. Despejamos una de las incógnitas en la ecuación lineal (ahora no podemos elegir la que queramos).

2ªecuación: y = 7- x

2º. Sustituimos su valor en la primera ecuación:

3º. Obtenemos una ecuación de segundo grado en una de las incógnitas (en este caso en x), la desarrollamos y resolvemos utilizando la fórmula conocida:

4º. Por último, como hemos obtenido dos valores de x, sustituimos en la ecuación que obtuvimos en el primer paso, obteniendo también dos valores de y:

Si x=3, y = 7-3=4

Si x=4, y = 7-3=4

5º. Las soluciones del sistema son: (3,4) y (4,3).

CASO 2: Si ambas ecuaciones son no lineales y ambas incógnitas son de segundo grado o en ambas ecuaciones la incógnita de segundo grado es la misma:

En este caso podemos resolver el sistema utilizando el método de reducción, aunque la ecuación que nos quede tras eliminar una de las incógnitas será una ecuación se segundo grado:

1º. Para poder eliminar una de las incógnitas (la x, por ejemplo) multiplicamos la primera ecuación por 2, y la segunda ecuación por -3.

2º. Resolvemos la ecuación que es una ecuación de segundo grado incompleta que nos da dos soluciones, que luego sustituiríamos en una de las ecuaciones para halla los valores de x.

3º. Como las raíces nos salen negativas, el sistema no tiene solución.

CASO 3: Ambas son ecuaciones no lineales, pero no de segundo grado, sino utilizando alguna función, ya sean logaritmos, exponenciales o la función inversa.

En este caso, resolveremos el sistema utilizando un método nuevo: el cambio de variable. Gracias a este método obtenemos un sistema más fácil de manejar, reduciéndose a uno de los casos anteriores:

1º. Realizamos el cambio de variable apropiado:

u=1/x, v=1/y.

2º. Escribimos el sistema en función de u y v:

3º. Como podemos observar, es un sistema del tipo que hemos mencionado en el caso 1, luego lo resolvemos por el método de sustitución. Por el que obtenemos los siguientes valores:

Si v = 2, u = 3,

Si v = -3, u = -2.

4º. Por último tenemos que deshacer el cambio: x=1/u, y=1/v. Por tanto las soluciones que obtenemos son: (1/3, 1/2) y (-1/2, -1/3)