Movimientos en el plano

Hoy vamos a estudiar los movimientos en el plano los cuales vienen dados por transformaciones geométricas. Una transformación geométrica es una aplicación del plano en sí mismo que a cada punto del plano asocia otro punto, conservándose tanto la forma como el tamaño de la figura u objeto que se mueve en nuestro plano, es decir; se conservan tanto los ángulos como las distancias. Hay tres tipos de movimientos: la traslación, el giro y la simetría. Además también pueden existir movimientos que resulten de la combinación de los anteriores.

TRASLACIONES

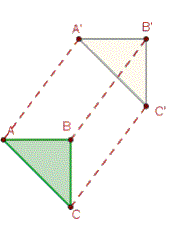Llamamos traslación a una transformación puntual, que lleva un punto del plano A, a otro punto A´. Por tanto se llama traslación de vector v=AA´. Se denomina como Tv, por tanto, Tv(A)=A´.

La traslación es un movimiento donde se conserva además la orientación. El punto A y el A´se dice que son homólogos.

-Propiedades de las traslaciones:

1. Las nuevas coordenadas del punto A´, se obtienen sumando el vector 0A, con el v. Es decir A´=Tv(A)=0A+v

Ejemplo: Si al punto A(3,1) le aplicamos una traslación de vector (2,2), entonces A´=Tv(3,1)=(3,1)+(2,2)=(5,3)

2. Si aplicamos una traslación a todos los puntos de una recta obtenemos una recta paralela a la original.

3. Si realizamos una traslación a una circunferencia de radio r y centro 0, obtenemos otra circunferencia que tendrá el mismo radio que la anterior y cuyo centro será el punto homólogo del anterior, es decir, 0´=Tv(0).

4. Cuando componemos dos traslaciones de vectores v1 y v2, obtenemos una traslación de vector la suma de los anteriores. A partir de la composición de traslaciones obtenemos algunos de los frisos o cenefas que se utilizan como motivos decorativos.

GIROS

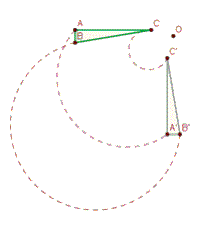
Llamamos giro de centro O y ángulo α a una transformación geométrica que hace corresponder a un punto P del plano otro punto P´, tal que, la distancia del centro a P es la misma que la distancia del centro al nuevo punto; y el ángulo que forman POP´es igual a α. Es decir d(OP) = d(OP´), por tanto se trata de un movimiento isométrico ya que conserva las distancias.

Diremos que un giro tiene sentido positivo cuando sea el contrario del sentido de las agujas de un reloj, en caso contrario, diremos que el sentido es negativo.

-Propiedades de los giros:

1. Si el ángulo de giro, α=180º, se denomina simetría central o simetría con respecto al origen.

2. Cuando giramos una figura alrededor de su centro O con un giro de 360º y se producen un número de n coincidencias, entonces se dice que esa figura tiene un centro de giro de orden n, y la figura es por tanto invariante de orden n.

3. Si componemos dos giros de mismo centro, O, y ángulo distintos α y β, entonces se obtiene un giro de centro O y ángulo α + β.

SIMETRÍAS

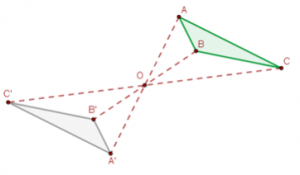
-Simetría central: Como ya hemos mencionado, se trata de un giro de centro O y de ángulo 180º. También podemos decir que una simetría central de centro O es un movimiento en el plano que transforma un punto A en otro A´siendo O el punto medio del segmento AA´.

Si componemos dos simetrías centrales con distinto centro, obtenemos una traslación.

-Simetría axial: Llamamos simetría axial de eje e a un transformación mediante la cual se le asocia a un punto del plano A otro punto A´, tal que el eje de simetría e es la mediatriz del segmento AA´, es decir; la distancia de A a la recta e es igual que la distancia del punto A´a la recta e: d(A,e)=d(A´,e).

Además, también se cumple, que la recta e será perpendicular al segmento que une A con A´.