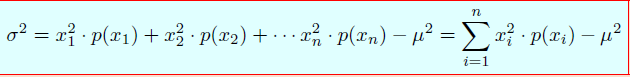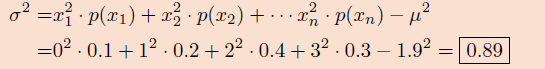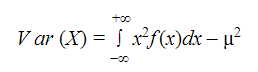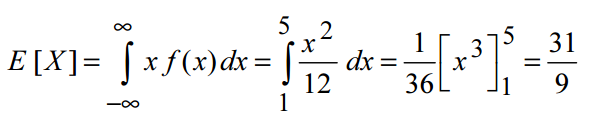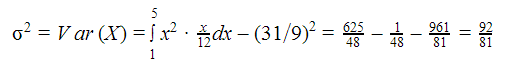Varianza matemática
Un concepto que está íntimamente ligado a la esperanza matemática es la varianza matemática. La varianza es una medida de dispersión, por tanto, se utiliza para estudiar el comportamiento de los valores de la variable aleatoria en función de la media (μ o E[x]), es decir, estudia lo alejado o no que están los valores de la media.
Definición: Llamamos varianza de una variable aleatoria X con media μ=E[x] a la esperanza del cuadrado de la diferencia entre la variable y su esperanza. Lo denotamos por Var[x] o σ^2:
Desarrollando esta expresión, obtenemos la fórmula que utilizamos normalmente para poder calcular la esperanza de forma práctica; dejando la de la definición para demostraciones o enunciados teóricos:
Propiedades: Sean a y b números reales (constantes) y X e Y variables aleatorias, entonces se cumplen las siguientes propiedades:
1. La varianza de una constante es nula: Var[a]=0.
2. La varianza de cualquier variable aleatoria siempre es positiva o cero: Var[X]≥0.
3. Las constantes salen de la varianza al cuadrado. Es decir, la varianza de una constante por una variable aleatoria es igual al cuadrado de la constante por la varianza de X: ![]()
4. La varianza de la suma de dos variables aleatorias independientes X e Y es igual a la suma de sus varianzas: Var(X+Y)=Var(X)+Var(Y).
5. Cuando las variables no son independientes se tiene que la suma de dos variables aleatoria es igual a la suma de las varianzas más dos veces la covarianza: Var (X+Y)=Var (X)+Var(Y)+2Cov(X,Y).
6. Como consecuencia de la primera y la tercera se deduce que: ![]()
DESVIACIÓN TÍPICA
Como la varianza es una medida de dispersión que tiene sus unidades al cuadrado, la variable que se utiliza normalmente para comparar los datos es la desviación típica, que no es otra cosa, que la raíz de la varianza; y por tanto se denota por σ.
VARIANZA PARA VARIABLES ALEATORIAS DISCRETAS
Sea X una variable aleatoria discreta con función de probabilidad P(X=x), y teniendo en cuenta la última fórmula dada para la varianza de una variable, obtenemos que:
Ejemplo: Tenemos un dado de cuatro caras, el cual tiene un número en cada cara el 0, 1, 2 y 3. El dado está trucado y no todos tienen la misma posibilidad de salir. Las probabilidades vienen dadas en la siguiente tabla.
A partir de estos datos halla la varianza de X y su desviación típica:
1º) En primer lugar siempre que nos pidan calcular la varianza tendremos que calcular la media:
2º) A continuación aplicamos la fórmula, recordando que tenemos que elevar cada valor que toma X al cuadrado y multiplicarlo por la probabilidad correspondiente:
3º) Para hallar la desviación típica, hacemos la raíz del resultado anterior:
VARIANZA PARA VARIABLES ALEATORIAS CONTINUAS
Sea X una variable aleatoria continua con función de densidad f(x), y (como hemos dicho en el caso anterior) teniendo en cuenta la última fórmula dada para el cálculo de la varianza; obtenemos que:
Ejemplo: Sabemos que la altura de un cierto árbol sigue una distribución continua con la siguiente función de densidad: f(x)=x/12, cuando 1<x<5. Hallar la varianza y la desviación típica.
1º) Los pasos a seguir son los mismos que en el caso anterior. Por tanto en primer lugar calculamos la media.
2º) Aplicamos la fórmula de la varianza:
3º) Para halla la desviación típica hacemos la raíz: