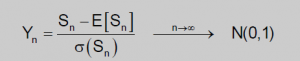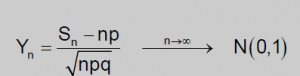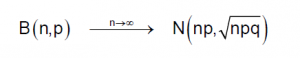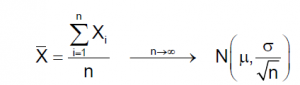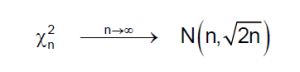Teorema central del límite

Vamos a estudiar hoy, uno de los teoremas más importantes que se utilizan en la suma de variables aleatorias de una sucesión en la que todas las variables siguen las misma distribución.

Este teorema nos viene a decir que la distribución de la suma de un número grande de variables aleatorias las cuales son independientes e idénticamente distribuidas (como ya hemos mencionado al comienzo), tienden a distribuirse o se pueden aproximar a una distribución normal.

De este teorema se conocen varias versiones (que realmente son casos particulares del primer teorema). Comenzaremos estas versiones y a continuación sus aplicaciones.

TEOREMA CENTRAL DEL LÍMITE (LINDEBERG-LEVY)

Sea {Xn} una sucesión de variables aleatorias independientes e idénticamente distribuidas (que denotaremos como v.v.a.a.i.i.d) con media y varianza finitas; y sea Sn la suma de n variables aleatorias de la sucesión: Sn=X1+…..+Xn. Entonces diremos que Sn converge a una normal, cuya media corresponde a la E[Xn] y cuya desviación típica (σ(Sn)) corresponde a la raíz de la Var[Xn]:

donde la E[Xn]=nE[X] (ya que la esperanza de la suma es la suma de las esperanzas y que como están idénticamente distribuidas, todas tienen la misma esperanza) y, análogamente, la Var[Xn]=nVar[X] (ya que la varianza de la suma es igual a la suma de las varianzas cuando las variables son independientes, y además todas tienen la misma varianza por estar idénticamente distribuidas.

Tipificando la expresión anterior, o, lo que es o mismo, definiendo una nueva sucesión de variables aleatorias {Yn} como el cociente de la diferencia entre la suma (Sn) y la esperanza de las suma y la desviación típica de Sn, obtenemos, que la nueva sucesión de variables aleatorias converge hacia una distribución Normal de media 0 y desviación típica 1: N(0;1):

TEOREMA CENTRAL DEL LÍMITE (DE MOIVRE-LAPLACE)

Esta versión del teorema central del límite se puede considerar como un caso particular cuando las variables aleatorias siguen una distribución de Bernouilli.

Teorema: Sea {Xn} una sucesión de v.v.a.a.i.i.d con distribución de Bernouilli de parámetro p : Xi→b(p), entonces, Sn=X1+X2+…….XN sigue una distribución Binomial de parámetros n y p: Sn→B(n;p). Como la esperanza de la binomial es n∙p y su varianza es n∙p∙q, entonces podemos decir que Sn converge a normal tal que:

Tipificando de la misma forma que en el caso anterior, obtenemos que la sucesión {Yn}, converge a una N(0;1).

APLICACIONES PRÁCTICAS DEL TEOREMA CENTRAL DEL LÍMITE

Por último, vamos a ver unas cuantas aplicaciones prácticas que nos serán de gran utilidad a la hora de realizar ejercicios con otras distribuciones.

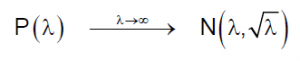
1. Aproximación asintótica de la Poisson a una Normal:

2. Aproximación asintótica de la Binomial a la Normal:

3. Aproximación asintótica de la media muestral de una una variable aleatoria de cualquier distribución donde vamos a denotar a la media de la variable aleatoria como: E[X]=μ, y la desviación típica de X como: σ:

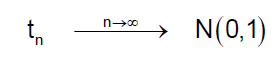
4. La distribución t-Student converge a una N(0;1):

5. La distribución Chi-cuadrado converge a una normal:

6. Aproximación asintótica de la Binomial mediante una Poisson:

siempre y cuando se cumpla que n≥30, np≤10 y p<0,1.