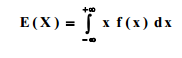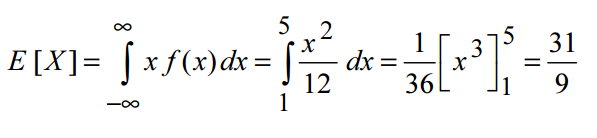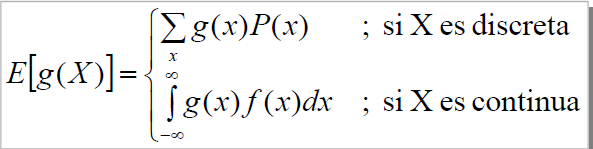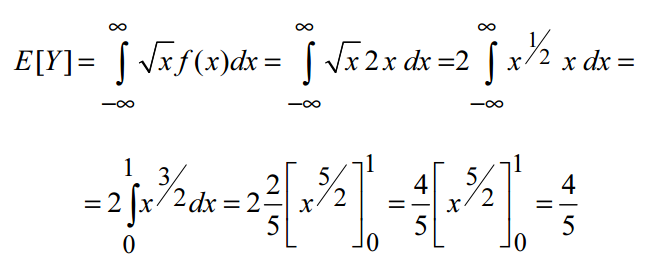Esperanza matemática
Vamos a estudiar un nuevo concepto estadístico, la esperanza matemática; estudiaremos sus características y la forma de obtención dependiendo si la variable estudiada es discreta o continua.
Definición: Llamamos esperanza matemática (también conocida como esperanza, valor esperado, media poblacional o simplemente media) al número que expresa el valor medio de un fenómeno aleatorio. Denotamos la esperanza de una variable aleatoria X como: μ=E[X].
La esperanza matemática es un concepto fundamental en la teoría de la probabilidad y la estadística. Es un valor que nos permite tener una idea de la tendencia central de una distribución de probabilidad, es decir, hacia dónde se concentran los valores. En términos más coloquiales, podríamos decir que la esperanza matemática es el valor que esperaríamos obtener si realizáramos un experimento un número infinito de veces.
Propiedades: Podemos decir que la esperanza es lineal, ya que cumple las propiedades lineales.
Dados a, b y c números reales (constantes), y sean X e Y variables aleatorias, se cumple:
1. La esperanza de una constante en la misma constante: E[c]=c.
2. La esperanza de la suma de dos variables aleatorias es igual a la suma de sus esperanzas:
E[ X+Y]=E[X]+E[Y].
3. La esperanza del producto de una constante por una variable aleatoria, es igual al producto de la constante por la esperanza de la variable aleatoria: E[aX]=aE[X].
4. De las propiedades anteriores se deduce que:
– E[aX+b]=aE[X]+b
– E[aX+bY]=aE[X]+bE[Y]
Estas propiedades de la esperanza matemática son muy útiles para simplificar cálculos y para demostrar resultados teóricos en estadística y probabilidad. Además, nos permiten entender mejor cómo se comportan las variables aleatorias y sus combinaciones.
ESPERANZA PARA VARIABLES ALEATORIAS DISCRETAS
Sea X una variable aleatoria discreta con función de probabilidad P(X=x), la esperanza de X viene dada por: E[X]=∑xi∙P(X=xi)=x1∙P(X=x1)+………+xn∙P(X=xn).
Las variables aleatorias discretas son aquellas que pueden tomar un número finito o contable de valores. Ejemplos de este tipo de variables son el número de caras obtenidas al lanzar un dado, el número de éxitos en una serie de ensayos de Bernoulli, entre otros.
Ejemplo: Vamos a jugar a un juego con nuestros amigos que consiste en lanzar dos monedas. Cuando salen dos caras recibimos 3 euros, si sale una cara recibimos 1 euro y si no sale ninguna cara pagamos 5 euros.¿Cuál es la ganancia media del juego?
1º) En primer lugar, tenemos que hallar la función de probabilidad. Para ello estudiamos los valores que toma nuestra variable aleatoria X y la probabilidad con que lo hace:
X={3,1,-5}
P(X=3)=P(salir dos caras)=1/2∙1/2=1/4.
P(X=1)=P(sacar una cara)=P(sacar cara y cruz)+P(sacar cruz y cara)= 1/2∙1/2+ 1/2∙1/2=2/4=1/2
P(X=-5)=P(no sacar ninguna cara o sacar dos cruces)=1/2∙1/2=1/4.
Por tanto la función de distribución queda de la siguiente manera:
Luego la esperanza es:
E[X]=3∙P(X=3)+1∙P(X=1)+(-5)∙P(X=-5)=3∙1/4+1∙1/2+(-5)∙1/4=0.
Observación: Si la media obtenida en un juego, que en este caso corresponde con el dinero que hemos ganado, es 0, entonces se denomina juego justo (ni ganas ni pierdes). Cuando la media es mayor que cero (μ > 0) se dice que es un juego con ventaja; y cuando la media es menor que cero ( μ < 0) es un juego en desventaja.
ESPERANZA PARA VARIABLES ALEATORIAS CONTINUAS
Sea X una variable aleatoria continua con función de densidad f(x), la esperanza de X se calcula como:
Las variables aleatorias continuas son aquellas que pueden tomar un número infinito de valores en un intervalo. Ejemplos de este tipo de variables son la altura de una persona, el tiempo que tarda un proceso, entre otros.
Ejemplo: Sabemos que la altura de un cierto árbol sigue una distribución continua con la siguiente función de densidad: f(x)=x/12, cuando 1<x<5. Calcular la E[X].
Para poder calcular la esperanza tenemos que resolver la integral, teniendo en cuenta que el límite inferior es 1 (el valor más pequeño que puede tomar x) y el límite superior es 5. Por tanto:
ESPERANZA MATEMÁTICA DE UNA FUNCIÓN DE VARIABLE ALEATORIA
Al igual que podemos calcular la esperanza o valor medio de una variable aleatoria, también podremos calcularla cuando se trate de una función de la variable.
En ese caso también distinguimos entre cuando se trate de una función con variable aleatoria discreta o cuando sea una función con variable aleatoria continua:
Ejemplo: La longitud de las extremidades de un cierto mamífero sigue una distribución continua con función de densidad: f(x)=2x si 1<x<2. Hallar la esperanza: 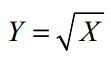
Luego, utilizando al definición para el caso continua, realizamos la integral entre los límites 1 y 2 obteniendo:
En resumen, la esperanza matemática es un concepto fundamental en la teoría de la probabilidad y la estadística. Nos permite entender mejor cómo se comportan las variables aleatorias y sus combinaciones, y es una herramienta esencial para la toma de decisiones en situaciones de incertidumbre.