Distribución binomial
De vuelta al mundo del azar y la probabilidad vamos a estudiar en esta ocasión la distribución binomial.
Definición: diremos que una variable aleatoria X, presenta una distribución binomial cuando repetimos n veces en las mismas condiciones un experimento de bernouilli; que es cualquier experimento en el cual sólo hay dos posibles resultados, llamados éxito y fracaso. En ese caso diremos que X sigue una distribución binomial de parámetros, n y p, y escribiremos: X→B(n;p)
Se trata de una variable aleatoria discreta, por tanto su función de probabilidad viene dada por:
Donde k representa el número de éxitos, p representa la probabilidad de que produzca éxito, y q=1-p, es la probabilidad de que se produzca el fracaso.
Un buen ejemplo de esta distribución es lanzar 100 veces una moneda y estudiar el número de caras, es evidente que estamos repitiendo un mismo experimento 100 veces, donde p = ½.
Propiedades:
1. La esperanza o media de una variable aleatoria binomial es el tamaño por la probabilidad del éxito: E[X]=n•p.
2. La varianza de una variable aleatoria binomial es el tamaño por la probabilidad del éxito y por la probabilidad del fracaso: Var(x)= n•p•q= n•p•(1-p). La desviación típica es la raíz de la varianza.
Para poder calcular una probabilidad, al igual que con la normal, también disponemos de unas tablas pudiendo utilizar bien la fórmula o bien la tabla, P(X=k). Además debemos tener cuidado, porque también puede ser que en alguna ocasión nos pidan calcular una probabilidad acumulada, es decir, P(X≤k).
Veamos un ejemplo de esta distribución y como podemos calcular una probabilidad mediante la fórmula, o por el contrario usando las tablas (lo cual resulta mucho más cómodo, por supuesto).
Ejemplo: La probabilidad de recibir un correo spam en un día es del 15%. Si un día recibimos 5 correos:
a) Calcula la probabilidad de que 3 de ellos sean spam.
b) Calcula la probabilidad de recibir más de 4 correos de tipo spam.
En primer lugar definimos la variable aleatoria y la distribución que sigue:
X=”Número de correos de tipo spam en un día”
n=5
p= P(recibir un correo spam)=0,15
Por tanto X→B(5; 0,15)
a) Tenemos que calcular: P(X=3)
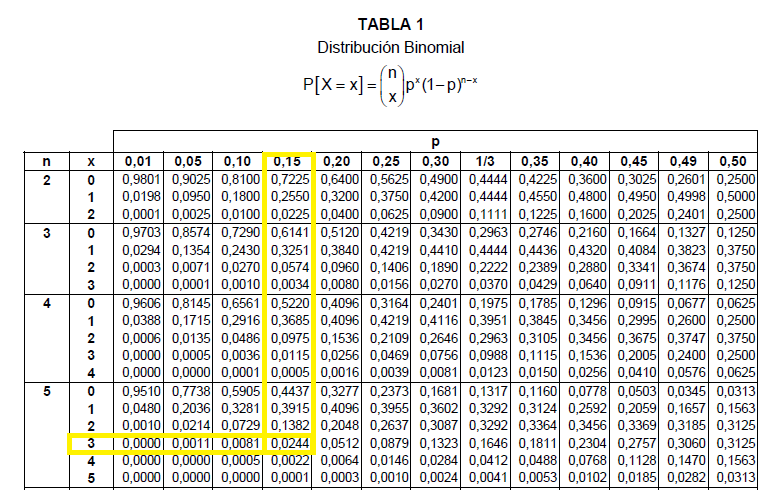
– Utilizando la tabla:
En primer lugar, nos fijamos en la columna de la izquierda que nos indica la n, y nos vamos hasta el n=5. Dentro de esa fila, hay una nueva columna que nos indica k, y elegimos la fila donde k=3. A continuación nos vamos a la primera fila donde nos da las probabilidades (p) y elegimos la columna donde p=0,15, tal y como se muestra en la imagen:
Por tanto P(X=3)=0,0244
b) Tenemos que calcular P(X>4)= 1- P(X≤4)
-Utilizando al fórmula:
P(X>4)=1-[P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4)]
Teniendo que aplicar la formula en cada caso.
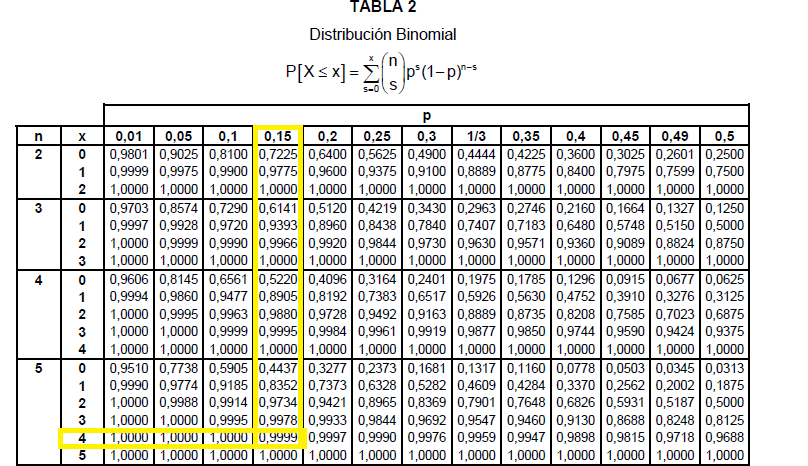
-Utilizando la tabla:
Cojamos ahora la tabla de la distribución acumulada: P(X≤x), y para buscar el número se procede de las misma forma que en el apartado a).
P(x>4)= 1- P(X≤4)=1- 0,9999=0,0001
Además, cuando el tamaño es lo suficientemente grande (n≥30), realizar algunos cálculos será muy difícil y costoso. Frente a esta situación utilizamos el teorema central del límite, que nos permite aproximar la distribución binomial a una más fácil y manejable como es la distribución normal.
Si X→B(n,p), ya hemos visto que E[X]=np y Var(X)=npq, por tanto, podemos decir:
X→N(np; √npq)
Dependiendo del nivel en el que estemos, deberemos llevar mucho cuidado, ya que como estamos pasando de una distribución discreta a una continua, tendremos que aplicar la corrección por continuidad.