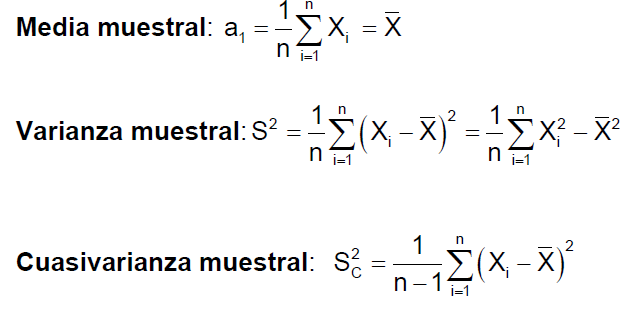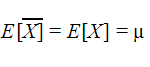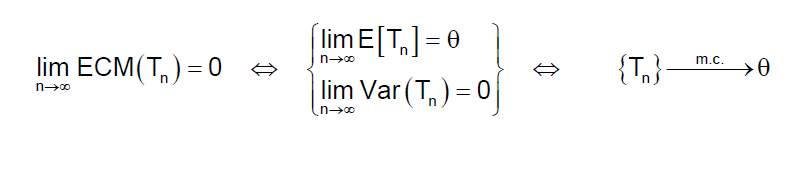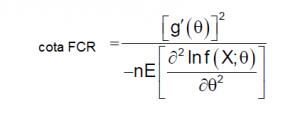Estimadores

Antes de comenzar con el estudio de los estimadores: su definición y sus propiedades; tenemos que comenzar viendo un concepto previo el de estadístico:

Definición: Sea una muestra aleatoria simple (m.a.s.) X1,X2,…Xn, llamamos estadístico a cualquier función real de la muestra siempre y cuando no contenga parámetros desconocidos: T(X1,X2…,Xn). Los estadísticos más comunes son la media muestral, la varianza muestral, la desviación típica muestral, la cuasivarianza muestral o la cuasidesviación típica muestral.

Observación: Los estadísticos se suelen denotar con letras mayúscula, mientras que los parámetros se denotan con letras griegas: μ, σ, λ,etc.

Una vez que ya hemos definido el concepto de estadístico, estamos preparados para estudiar los estimadores.

Definición: Diremos que un estadístico T(X1,X2,…,Xn) es un estimador del parámetro θ si cumple:

1. Que T(X1,X2,…Xn) no contiene ningún parámetro desconocido.

2. Si para cualquier realización muestral (x1,x2,….xn) entonces T(x1,x2,….xn) pertenece al campo de variación del parámetro, es decir, es un posible valor para nuestro parámetro θ.

Si nuestra función cumple estas condiciones diremos que T(X1,X2,…Xn) es una estimación de θ.

PROPIEDADES DESEABLES DE LOS ESTIMADORES

Un estimador será mejor para aproximar el valor de nuestro parámetro cuantas más propiedades de las siguientes cumpla.

-Insesgadez

Diremos que un estimador T de θ es insesgado si la esperanza del estimador coincide con el parámetro que estamos estimando: E[T]= θ.

En caso contrario diremos que T es un estimador sesgado de θ, y denominamos sesgo b( θ) como la diferencia entre la esperanza del estimador y el parámetro que estamos estimando: b(θ)= E[T]- θ.

Ejemplo: La media muestral es un estimador insesgado para la media poblacional: μ, para cualquier población ya que la esperanza de la media muestral coincide con la de la media poblacional:

-Insesgadez asintótica

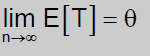
Diremos que un estimador T de θ es asintóticamente insesgado, cuando el límite de la esperanza del estimador coincida con el parámetro estimado:

Observación: Si T es un estimador insesgado de θ, entonces es asintóticamente insesgado.

-Consistencia en media cuadrática

Diremos que un estimador T de θ es consistente si converge en media cuadrática a θ. De forma práctica, tenemos que demostrar que cumpla:

1. Que el límite de la esperanza coincida con el parámetro (asintóticamente insesgado).

2. Que el límite de la varianza sea cero:

-Eficiencia:

Diremos que un estimador T es eficiente para θ si se cumple que:

1. Sea un estimador insesgado.

2. La varianza del estimador coincida con la cota de Fréchet-Cramer-Rao: Var(T)=cota F.C.R.

Donde la cota de Fréchet-Cramer-Rao se define como:

donde g´(θ )=1.

-Eficiencia asintótica:

Diremos que T es un estimador asintóticamente eficiente de θ si:

1. Es asintóticamente insesgado, es decir, el límite de la esperanza del estimador coincide con el parámetro que estamos estimando.

2. El límite entre la varianza del estimador y la cota de F.C.R es 1.

-Estimador insesgado de mínima varianza uniforme (E.I.M.V.U)

Diremos que un estimador T* insesgado para θ con varianza finita es E.I.M.V.U si la varianza de T* es menor o igual que la varianza de cualquier T insesgado para θ: Var(T*)≤ Var(T).

Observación: Si T es un estimador eficiente, entonces es E.I.M.V.U.