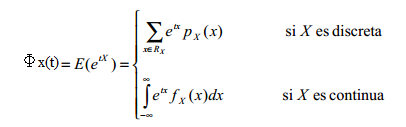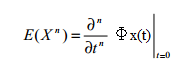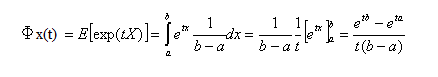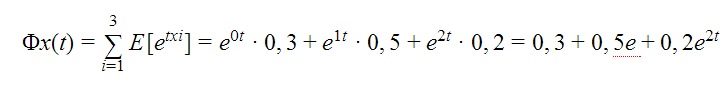Función generatriz de momentos

Vamos a estudiar en esta ocasión un nuevo concepto estadístico, la función generatriz de momentos. La importancia de esta nueva función se debe a su unicidad, además gracias a ella podemos determinar completamente la distribución de una variable aleatoria. Pero antes, recordaremos cuáles eran los momentos de una variable aleatoria:

Definición: Llamamos momento de orden r de la variable aleatoria X a la esperanza de la potencia r-ésima de la variable aleatoria: E[X^r].

Obviamente, el caso particular de r=1, es decir, el momento de orden uno, coincide con al esperanza.

FUNCIÓN GENERATRIZ DE MOMENTOS

Definición: Se define la función generadora de momentos o función generatriz Фx(t) de una variable aleatoria X como la esperanza de e elevado al producto t∙x, donde t puede ser cualquier número real siempre y cuando la función obtenida sea derivable.

Dependiendo del carácter de la función (discreta o continua) la función generatriz se obtendrán por medio de un sumatorio o de una integral:

El nombre de la función se debe a la estrecha relación que existe entre ella y los momentos de la variable aleatoria X. Ya que los momentos de orden n pueden ser obtenidos haciendo la derivada n-ésima de la función y sustituyendo el valor de t=0, tal como se enuncia en el siguiente teorema:

Teorema: Dada una variable aleatoria X, de la cual podemos calcular su función generatriz, Фx(t), entonces se cumple que:

PROPIEDADES

Algunas de las propiedades más importantes y que más usos tienen son:

1. Dada una variable aleatoria X con función generatriz Фx(t) , entonces si hacemos un cambio de origen en la variable, Y=X+ a, entonces la función generatriz de momentos de la nueva variable Y es: Фy(t)=e^at∙Фx(t).

2. Dada una variable aleatoria X con función generatriz Фx(t), si hacemos un cambio de escala, Y=aX, entonces la función generatriz de momentos de la nueva variable aleatoria es:

Фy(t)=Фx(at).

3. Uniendo las dos propiedades anteriores; si realizamos un cambio de origen y de escala en la variable aleatoria Y=aX+b, entonces la función generatriz de la nueva variable es: Фy(t)=e^bt∙Фx(at).

4. Si dos variables aleatorias tienen la misma función generatriz, entonces las dos variables tienen la misma distribución.

5. Dada dos variables aleatorias con funciones de momentos respectivas Фx(t) y Фy(t), entonces la función generatriz de la variable aleatoria obtenida al sumar las dos variables anteriores, Z=X+Y, es el producto de las anteriores: Фz(t)=Фx+y(t)= Фx(t) ∙ Фy(t).

Además de estas propiedades, es importante tener en cuenta que la función generatriz de momentos no siempre existe. Para que exista, la esperanza de e^tx debe ser finita para todo t en un intervalo abierto que contenga al cero. En caso contrario, la función generatriz de momentos no está definida.

Ejemplo 1: Halla la función generatriz de momentos de una variable aleatoria continua que sigue una distribución uniforme de parámetro a y b: X:U(a,b).

Como estamos en el caso de variables aleatorias continuas tenemos que utilizar la fórmula que implica la integral de la función de densidad de la variable. Por tanto, en primer lugar tenemos que escribir la función de densidad: f(x)=1/(b-a).

Resolviendo la integral tenemos que:

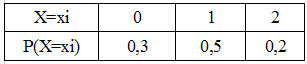
Ejemplo 2: Halla la función generatriz de momentos de la siguiente variable aleatoria discreta cuya función de probabilidad viene dada por:

Utilizando la fórmula que hemos mencionado al comienzo obtenemos:

Es importante notar que la función generatriz de momentos es una herramienta muy útil en el estudio de las distribuciones de probabilidad. Nos permite obtener los momentos de una distribución de una manera más sencilla y directa que calculándolos directamente a partir de la definición. Además, nos proporciona una forma de comparar diferentes distribuciones y de obtener nuevas distribuciones a partir de las existentes. Sin embargo, como se mencionó anteriormente, no siempre existe, por lo que no siempre podremos utilizarla.