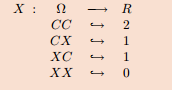Variable aleatoria discreta

Tanto hablar de Estadística, y me acabo de dar cuenta que el concepto principal para cualquier tema, todavía no lo hemos definido, ¡vaya despiste!

Por tanto, hoy por fin, vamos a estudiar las variables aleatorias, que como ya hemos mencionado en varias ocasiones hay de dos tipos: discretas y continuas. Nos centraremos en primer lugar en el estudio las de tipo discreto: para qué las utilizamos, cómo las definimos, cuáles son sus características más importantes, así como algún ejemplo que nos facilite la comprensión; y dejaremos para el próximo día el estudio de las variables de tipo continuo.

Pero antes, comenzaremos dando la definición general para cualquier variable aleatoria.

Definición: Una variable aleatoria es cualquier función que hacemos corresponder a un determinado experimento aleatorio, mediante la cual asociamos a cada elemento del espacio muestral, que denotamos por Ω, un número real: X: Ω →R.

Llamamos rango de una variable aleatoria a la imagen de la función anterior, es decir, los números reales que puede tomar nuestra variable aleatoria: R={xεR/ existe ωε Ω: X(ω)=x}.

Para denotar las variables aleatorias utilizamos letras mayúsculas, mientras que para designar los valores concretos de las mismas utilizamos las letras minúsculas.

VARIABLES ALEATORIAS DISCRETAS

Una variable aleatoria discreta es aquella que asociamos a experimentos a aleatorios donde la variable sólo puede tomar valores enteros; aunque en algunas ocasiones también pueden ser decimales siempre y cuando estén dentro de un rango concreto. Por ejemplo si X={2; 2,5; 3; 3,5}, en este caso se trata de una variable discreta porque X no puede tomar ningún valor entre medias.

Algunos de los ejemplos para los que utilizamos este tipo de variables es cuando estudiamos el número de hijos o hermanos de una familia, el número obtenido al lanzar un dado, etc.

Ejemplo: Si lanzamos dos monedas, hallar la variable aleatoria X que estudia el número de caras.

1º) En primer lugar, estudiamos el espacio muestral: Ω={XX,CC,XC,CX}, (donde X corresponde a sacar cara y evidentemente, C corresponde a sacar cara)

2º) Definimos nuestra variable aleatoria como la siguiente aplicación: X: Ω →R

Función de probabilidad:

Una variable aleatoria discreta viene determinada por su función de probabilidad: P(X=x), que es una aplicación que asocia a cada valor x de la variable aleatoria X, la probabilidad de que la variable tome ese valor. Por tanto, es una aplicación que tiene como conjunto de partida la variable X y como conjunto de llegado el intervalo [0,1], ya que la probabilidad tiene que estar entre esos valores: P(X=x): X→[0,1].

Propiedades: Si llamamos Pi=P(X=xi) para cada xi perteneciente a la variable aleatoria X, se tiene que:

a) Por ser una probabilidad: 0≤Pi≤1

b) La suma de todas las probabilidades tiene que ser 1: ∑Pi=1.

c) Se representa mediante un diagrama de barras.

Ejemplo: A partir del caso anterior, cuando lanzamos dos monedas, estudiar la función de probabilidad para la variable aleatoria X={número de caras}

1º) En primer lugar definimos la variable aleatoria (lo cual hemos hecho en el ejemplo anterior), para saber los valores que puede tomar. Luego, X={0,1,2}

2º) Estudiamos la probabilidad para cada uno de los casos:

P(X=0)=P(sacar dos cruces)=1/2∙1/2=1/4

P(X=1)=P(sacar 1 cara)=P(sacar cara y cruz)+P(sacar cruz y cara)= 1/2∙1/2+ 1/2∙1/2=2/4=1/2

P(X=2)=P(sacar 2 caras)= 1/2∙1/2=1/4

Por tanto la función de probabilidad que la representamos mediante una tabla queda de la siguiente manera: