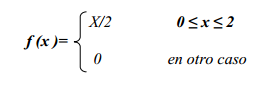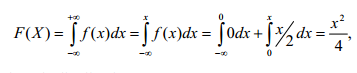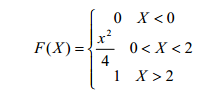Función de distribución

6 de febrero de 2013 Publicado por Laura

Volvemos de nuevo al campo de la Estadística, en este caso, vamos a estudiar la función de distribución, cuáles son sus propiedades, y como se calcula cuando trabajamos con variables de tipo discreto, así como cuando trabajamos con variables de tipo continuo.

DEFINICIÓN

Llamamos función de distribución de una variable aleatoria X y la denotamos por F(x), a la función que asocia a cada valor x la probabilidad acumulada para todos los valores menores o iguales a x: F(x)=P(X≤x).

Podemos decir por tanto, que la función de distribución nos permite estudiar el comportamiento probabilístico de la variable aleatoria X que tiene asociada cualquier experimento aleatorio.

PROPIEDADES

Cualquier función que cumpla estas cinco propiedades diremos que es un función de distribución, y recíprocamente; toda función de distribución tiene que cumplir estas cinco propiedades por el simple hecho de ser función de distribución:

1. Su imagen está entre el 0 y el 1. 0≤F(x)≤1.

2. Para valores de la variable aleatoria en el más infinito (los valores mayores de los que están definidos), la función de distribución tiende a 1: F(x)→1 cuando x→+∞. Es decir:

3. Por el contrario, para los valores de la variable aleatoria en el menos infinito (los valores más pequeños de los que están definidos), la función de distribución tiende a cero: F(x)→0 cuando x→-∞. Es decir:

4. F(x) es un función monótona creciente, es decir, si x1<x2, entonces F(x1)≤F(x2).

5. F(x) es continua por la derecha, por tanto se cumple:

REPRESENTACIÓN

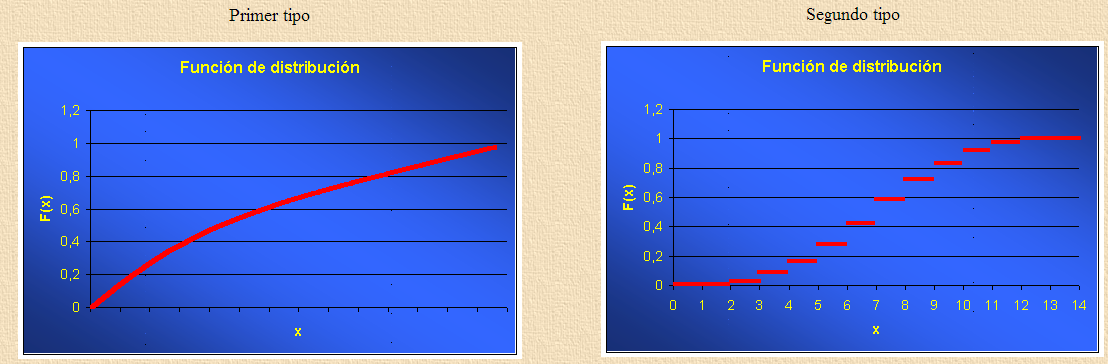
A partir de las propiedades anteriores, podemos decir como será la representación de nuestra función. Nos podemos encontrar dos tipos de representaciones, y en algún caso, puede ser que sea una mezcla se ambas.

FUNCIÓN DE DISTRIBUCIÓN EN VARIABLES ALEATORIAS DISCRETAS

Veamos ahora cómo calcular la función de distribución cuando X sea una variable aleatoria discreta que viene dada por su función de probabilidad P(X=x).

F(xk)=P(X≤xk)=∑xi P(X=xi)=x1P(X=x1)+……..+xkP(X=xk)

Es decir, tenemos que realizar el sumatorio de los productos que las probabilidades hasta llegar al valor de la variable aleatoria indicado.

Ejemplo: Hallar la función de distribución de la siguiente variable aleatoria que viene dada por la siguiente función de probabilidad:

Como nuestra variable aleatoria toma valores entre el 4 y el 6,5; nuestra función de distribución cuando x<4, entonces F(x)=0. Y cuando x≥6,5 entonces F(x)=1.

Para hallar el resto, los iremos sumando, ya que tenemos que ir hallando las probabilidades acumuladas, de tal forma que:

FUNCIÓN DE DISTRIBUCIÓN EN VARIABLES ALEATORIAS CONTINUAS

En el caso de las variables continuas, las cuales vendrán definidas por su función de densidad f(x), que es no negativa e integrable; luego, para poder hallar la función de distribución tendremos que realizar la siguiente integral:

Ejemplo: Hallar la función de distribución de una variable aleatoria X, cuya función de densidad es la siguiente:

En este caso, la variable aleatoria toma valores entre 0 y 2, por tanto cuando x<0, entonces F(x)=0, y en el caso de que x≥2, entonces F(x)=1. Para los demás casos, realizamos la integral:

Por tanto, la función de distribución es: