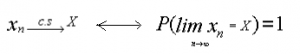Tipos de convergencia

En el artículo de hoy vamos a estudiar los diferentes tipos de convergencia de las sucesiones de variables aleatorias, es decir, las propiedades asintóticas de las mismas. Para ello, comenzaremos recordando la definición de sucesión de variables aleatorias.

Definición: Una sucesión de variables aleatorias es un conjunto infinito numerable de variables aleatorias X1, X2,…….Xn,…..que denotaremos por {Xn}, donde cada Xi tiene una función de distribución asociada.

1. CONVERGENCIA CASI SEGURA

Dada la sucesión de variables aleatorias {Xn}, diremos que convergen de forma casi segura (o con probabilidad 1) a una variable aleatoria X cuando la probabilidad de que el límite de la sucesión de variables aleatorias (xn) sea la variable aleatoria a la que converge (x) sea 1:

Observación: Puede ocurrir que nuestra sucesión {Xn} converja a una constante K, tanto en este tipo de convergencia como en todos los demás.

2. CONVERGENCIA EN LEY O EN DISTRIBUCIÓN

Sea {Xn} una sucesión de variables aleatorias y sean Fn(x) sus funciones de distribución respectivas. Diremos que {Xn} converge en Ley o distribución a una variable aleatoria X con función de distribución F(x), si se cumple que el límite cuando n tiende a ∞ de Fn(x) es F(x) para todos los puntos de continuidad de F(x):

Observaciones: Se dice que {Xn} se distribuye asintóticamente como X. A la función F(x) la llamamos función de distribución límite de Xn.

3. CONVERGENCIA EN PROBABILIDAD

Diremos que una sucesión de variables aleatorias {Xn} converge en Probabilidad a una variable aleatoria X cuando se cumpla que el límite de la probabilidad de que los valores de la sucesión Xn estén tan próximos a X como se desee (ε) sea 1. O bien, utilizando el recíproco, cuando el límite de la probabilidad de que los valores de la sucesión Xn y los de la variable aleatoria X difieran en un valor tan pequeño como se desee (ε) sea 0:

Observación: Este tipo de convergencia lo podríamos interpretar considerando que a partir de un cierto valor n en adelante todos los valores de la sucesión de variables aleatorias {Xn} se aproximan a X con mayor probabilidad.

Puede ocurrir que nuestra sucesión {Xn} converja a una constante K, tanto en este tipo de convergencia como en todos los demás.

4. CONVERGENCIA EN MEDIA CUADRÁTICA

Por último, diremos que una sucesión de variables aleatorias {Xn} con momentos de orden r finitos, diremos que converge en media cuadrática a una variable aleatoria X, con momentos de orden r finitos, cuando el límite de la dispersión de {Xn} respecto a la variable aleatoria X, converja a 0:

Observación: En este caso la interpretación de este tipo de convergencia nos dice que la distancia cuadrática media entre una sucesión de variables aleatorias {Xn} y la variable aleatoria a la que converge X se hace tan pequeña como se quiera de un n en adelante.

Podemos considerar diferentes tipos de convergencia en media cuadrática dependiendo del orden del momento elegido. Comúnmente, al igual que en el ejemplo, se utilizará el de orden 2.

Para entender mejor estos conceptos, es útil considerar algunos ejemplos. Supongamos que tenemos una sucesión de variables aleatorias que representan los lanzamientos de una moneda. Si lanzamos la moneda un número infinito de veces, esperamos que la proporción de caras converja a 0.5. Esto es un ejemplo de convergencia en probabilidad.

Por otro lado, si consideramos una sucesión de variables aleatorias que representan los lanzamientos de un dado, y definimos la variable aleatoria X como la suma de los resultados de los lanzamientos dividida por el número de lanzamientos, entonces esperamos que X converja a 3.5, que es el valor esperado de un lanzamiento de un dado. Esto es un ejemplo de convergencia en ley o en distribución.

RELACIONES ENTRE LOS TIPOS DE CONVERGENCIA

Una vez que ya hemos visto los diferentes tipos de convergencia que pueden darse en las sucesiones de variables aleatorias, veremos las relaciones que existentes entre ellos:

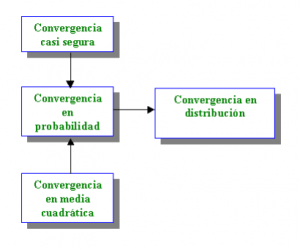
1. Si una sucesión {Xn} converge en media cuadrática a X, entonces esta sucesión también convergerá en probabilidad. El recíproco, normalmente no es cierto.

2. Si una sucesión {Xn} converge de forma casi segura a una variable aleatoria X, entonces {Xn} converge en probabilidad. Al igual que el anterior, el recíproco (normalmente) no es cierto.

3. Por último, si {Xn} converge en probabilidad a X, entonces {Xn} converge en ley o distribución. El recíproco, en este caso, tampoco se cumple de manera general.

Estas relaciones se pueden apreciar en el siguiente esquema:

Es importante tener en cuenta que estas relaciones no son bidireccionales. Es decir, si una sucesión de variables aleatorias converge en un sentido, no necesariamente converge en los otros sentidos. Esto es lo que hace que el estudio de la convergencia sea un tema tan fascinante y complejo en la teoría de la probabilidad.