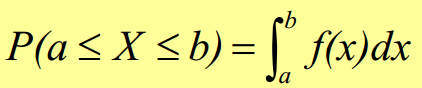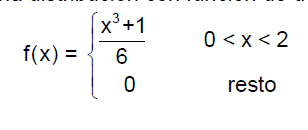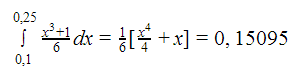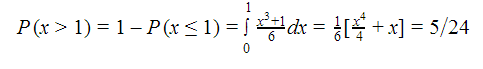Variable aleatoria continua

Ya sabéis que todo lo que se promete hay que cumplirlo, por tanto… hoy continuamos con el post de ayer, y vamos a estudiar las variables aleatorias de tipo continuo. De la misma forma que ayer, veremos para qué las utilizamos, cómo las definimos, las características más importantes y como no podía faltar, un ejemplo que nos ayude en la comprensión de lo expuesto anteriormente.

VARIABLES ALEATORIAS CONTINUAS

Una variable aleatoria continua es aquella que asociamos a experimentos a aleatorios donde la variable puede tomar todos los valores que se encuentran dentro de un intervalo, por tanto, podrían ser con infinitos decimales. Por tanto, para realizar el estudio de muchas de sus características es necesaria obtener la marca de clase, que denotamos por x, y que corresponde al punto medio del intervalo.

Algunos de los ejemplos más comunes que modelizamos utilizando variables aleatorias continuas son el peso o la altura de una persona, la duración de un trayecto, etc; cuyo rango de precisión puede ser infinito.

Ejemplo: Preguntamos en una clase de 15 alumnos las notas que han sacado en un examen y obtenemos los siguientes resultados: 3,5-5,75-8-9,25-7,05-6,5-2,55-4,25-6-5,9-1,25-8-8,75-5,65-4,55.

Para escribir nuestra variable aleatoria, es necesario agrupar los datos en intervalos, de tal forma que:

X={(0,2],(2,4],(4,6],(6,8],(8,10]}

Función de densidad

En el caso de las variables aleatorias continuas vienen definidas por la función de densidad, que denotamos por f(x), y que sería la función análoga a la función de probabilidad en el caso de las variables discretas. Nos proporciona la posibilidad relativa de que la variable aleatoria X tome un valor próximo a x.

Propiedades: Sea f(x) la función de densidad de una variable aleatoria X se cumple que:

a) La función de densidad siempre es positiva para todo valor que cualquier valor real que tome x: f(x)≥0 con -∞<x<+∞.

b) La integral en -∞ y +∞ de la función de densidad vale 1 (es la análoga de que la suma de las funciones de probabilidad en las discretas es 1):

c) Para calcular la probabilidad entre dos número hay que resolver la siguiente integral:

Ejemplo: En un pequeño comercio de barrio donde se venden componentes electrónicos, se distribuyen entre otro productos, cable telefónico. El número de metros de un determinado tipo (en miles de metros) sigue una distribución con función de densidad:

a) ¿ Cuál es la probabilidad de que el mes próximo venda entre 100 y 250 metros de cable?

b) Si, al comienzo del mes, la tienda dispone de un stock de 1000 metros de cable, ¿cuál es la probabilidad de que no se puedan atender a todos los clientes que solicitan este artículo?

a)Para poder calcular la probabilidad pedida tenemos que utilizar la propiedad 3 de la función de densidad.

Tened mucho cuidado, ya que nuestra función de densidad viene dada en miles de metros (es decir en kilómetros), por tanto nos están pidiendo la probabilidad de que 0,1<x<0,250: P( 0,1<x<0,250).

Resolvemos la integral siguiente:

b) Como en este caso nos pide que no se pueda atender a todo el mundo, tenemos que calcular P(x>1):