Función gaussiana
La función gaussiana, se denomina de tal forma en honor al matemático, astrónomo y físico alemán Carl Friedrich Gauss. Esta es una función que se puede definir mediante la siguiente expresión:
![]()
donde a, b y c corresponden a constantes reales (a > 0).
La gráfica de la función es simétrica y su forma es de campana, por esta razón se denomina generalmente campana de Gauss. El parámetro a es correspondiente al alto de la campana que se centra en el punto b, estableciendo c la anchura de la misma.
Veamos ahora como sería la gráfica de la campana de Gauss;
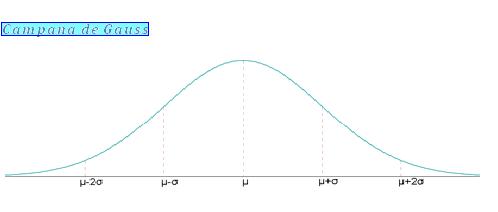
La característica mas elemental de la curva en cuestión es que es una necesaria y muy buena forma de representar la distribución de variables aleatorias en localidades y ciudades. Por esta razón es muy util para realizar cálculos de estadística.
Además, la función gaussiana tiene una amplia gama de aplicaciones en diversas disciplinas científicas y técnicas. En la física, por ejemplo, se utiliza en la teoría cuántica de campos, donde las funciones gaussianas se utilizan para describir el estado de un sistema en un momento dado. En la química, las funciones gaussianas se utilizan en la teoría del funcional de la densidad para describir la densidad electrónica de un sistema. En la ingeniería eléctrica, las funciones gaussianas se utilizan en el análisis de señales y sistemas.
Es correspondiente en el caso de que a sea igual a lo siguiente,
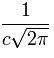
a la función de la densidad perteneciente a una variable aleatoria con repartimiento normal de,
Media o valor medio,
![]()
Varianza,
![]()
En el campo de la estadística, la función gaussiana se utiliza para describir la distribución de los datos. Esta distribución, conocida como la distribución normal, es la más comúnmente utilizada en estadística. La razón de esto es que muchas variables aleatorias en la naturaleza siguen una distribución normal. Por ejemplo, las alturas de las personas, los resultados de los exámenes y los errores de medición suelen seguir una distribución normal.
Las funciones gaussianas del tipo,
![]()
son las autofunciones de la transformada de Fourier. Esto quiere decir que la transformada de Fourier de una función gaussiana corresponde también a un múltiplo escalar de la función original.
Las gaussianas están entre las funciones elementales, (funciones construidas a partir de una cantidad finita de exponenciales, constantes,variables, logaritmos y raíces de ecuaciones por medio de la composición y formas de combinación, usando las cuatro operaciones elementales ) aunque no tengan primitivas primordiales. Pese a esto, el valor exacto de la integral impropia sobre todo el rango real es posible que resulte a partir del valor de la integral de Gauss (también llamado integral de probabilidad) obteniéndose lo siguiente:
![]()
El valor de la integral corresponde a uno únicamente si,
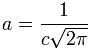
La primitiva (función construida a partir de una cantidad finita de exponenciales) de una función gaussiana correspondiente a la llamada función error de Gauss. Esta es una función no elemental la cual puede verse en muchos argumentos de las ecuaciones diferenciales, ingeniería, probabilidad, estadística, ciencias matemáticas, ciencias sociales y ciencias naturales.
Además, la función gaussiana también tiene aplicaciones en el procesamiento de imágenes y señales. En este contexto, se utiliza para suavizar o desenfocar una imagen, lo que puede ser útil para reducir el ruido o para preparar la imagen para un análisis posterior. En el procesamiento de señales, la función gaussiana se utiliza para modelar el efecto de un sistema de comunicación sobre una señal transmitida.
