Valor absoluto

Cualquier número puede ser representado en una recta real. El valor absoluto o módulo de un número, constituye la distancia de un punto a al origen. Podemos observar en la recta que se muestra a continuación que la distancia del 3 al origen es 3. De igual forma la distancia del punto -3 al origen también es 3. Esto se apuntaría de la siguiente forma:

│-3│=3

Las barras son leídas como el valor absoluto de lo que está dentro. Sin importar en cual de los lados de la recta real se representa el número. Metódicamente podemos ver que si a es positivo, o sea si se encuentra a la derecha de cero, entonces,

│a│=a

Mientras que si se encuentra a la izquierda del origen, es decir si a es negativo, tenemos que,

│a│=-a

Lo escribimos de este modo,

El valor absoluto de un número real x, es definido como:

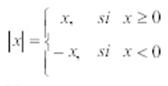
Veamos algunos ejemplos:

Podemos observar como el valor absoluto a una cantidad positiva permanece igual mientras que a una cantidad negativa le cambia el signo.

La expresión a la cual le estamos tomando valor absoluto es de signo positivo por lo cual el valor absoluto queda igual. Aquí se utilizó la primera parte de la definición.

Si la expresión a la cual le estamos hallando valor absoluto es de signo negativo, el valor absoluto cambiará el signo. Aquí se utiliza la segunda parte de la definición.

Ecuaciones con valor absoluto

Si x es una incógnita en la expresión, entonces no se sabe si x-3 es positivo o negativo. Pero si tenemos la ecuación:

│x-3│=5

Debemos tomar en cuenta las dos posibilidades que tenemos de signo, por lo cual hay dos opciones,

1) x-3=5

2) x-3=-5

La primera opción se da en el caso en que x-3 sea positivo, la segunda opción se da en caso que sea negativo.

Si resolvemos la ecuación tenemos que:

1) x=8

2) x=-2

Consecuentemente estos valores de x satisfacen la ecuación:

│x-3│=5

Las propiedades fundamentales del valor absoluto son:

a) No negatividad

b) Definición positiva

c) Propiedad multiplicativa

d) Propiedad aditiva

Valor absoluto de un número complejo

Un números complejo corresponde a la suma de un número real y un número imaginario. No representan un conjunto que se conforma por una relación binaria de orden parcial en el sentido de los números reales, por lo cual se puede decir que los números complejos no conforman un conjunto ordenado. Se utiliza para este caso una nueva identidad que proporcione entonces otra opción para la definición de valor absoluto si hablamos de complejos. Entonces:

para cualquier número complejo de la siguiente forma,

con x e y como números reales, el valor absoluto de z se define de esta manera: