Función signo
La función signo es una función definida a trozos o función por partes, la cual es representada habitualmente por medio de sgn(x). Se requiere de varias fórmulas para poder definirlas, cada una de las cuales establece el comportamiento de la función en un cierto fragmento o trozo. La definición cambia según el valor de la variable independiente y esta no depende de ningún factor para cambiar. Una función real f (definida a trozos) de una variable real x es correspondiente a una relación cuya definición es concebida por varios conjuntos disjuntos de su dominio los cuales se denominan subdominios.
Una función es diferenciable a trozos si cada trozo es diferenciable a lo largo de todo el dominio.
Entonces podemos definir la función signo de las siguientes formas, veamos:
1. Si su conjunto de definición, conjunto de partida o dominio de definición es R y su conjunto imagen {-1;0;1}, o sea:
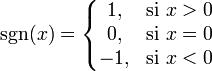
2. A manera de derivada de la función valor absoluto. Su dominio de definición es R – {0} y su conjunto imagen Im={-1;1}
![]()
La derivada constituye cómo una función cambia (valor de la variable dependiente) a medida que su entrada también cambia.
3. sgn(x) = 2u(x) – 1 donde u es la función escalón unitario o Heaviside Step (denominada así en honor al matemático ingles Oliver Heaviside) que se define de la siguiente forma:
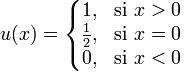
Propiedades de la función signo
• La función signo es una función impar, o sea:
![]()
Podemos clasificar a las funciones según su paridad. Las funciones pueden ser pares, impares o no tener paridad. Esto se debe a la paridad de las potencias de las funciones de potencia que integran cada condición:
La función x elevada a n
a- es una función par si n es un entero par,
b- es una función impar si n es un entero impar.
• Todo número real x puede expresarse como producto de su módulo o valor absoluto y la función signo evaluada en x.
![]()
El valor absoluto de un número real es su valor numérico sin tener en cuenta su signo.
• La función signo corresponde a la derivada de la función valor absoluto, (con independencia en cero).
![]()
• Es derivable con derivada 0 para todo su dominio con excepción de 0.Pero No es derivable en 0 en el sentido común de derivada.
La función Delta de Dirac es una función generalizada o distribución, fue descubierta y utilizada por primera vez por el físico teórico británico Pail Dirac. Esta función es importante en la teoría de las distribuciones (tambien se conoce como función generalizada) ya que la derivada de la función signo puede ser dos veces la función delta de Dirac.
![]()
