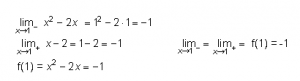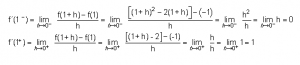Derivabilidad de una función
Como ya estudiamos en otra ocasión la función derivada, hoy nos vamos a centrar simplemente en la derivabilidad de las funciones (que se puede considerar un estudio análogo a la continuidad de una función, pero en este caso utilizando su derivada). Comenzaremos viendo la definición, los diferentes tipos que nos podemos encontrar y su interpretación.
Definición: Diremos que una función f(x) definida en un entorno A de la recta real es derivable en un punto a perteneciente a A si y sólo si existe la función derivada en ese punto. Diremos que la función f(x) es derivable en el intervalo A cuando sea derivable en todos los puntos de A.
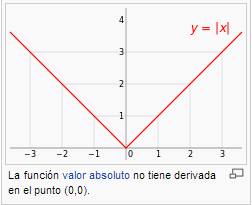
Observación: Si una función es derivable, entonces es continua. Mientras que el recíproco no es cierto, una función puede ser continua y no tiene por qué ser derivable, como es el caso de la función valor absoluto: f(x)=|x|.
PASOS PARA ESTUDIAR LA DERIVABILIDAD.
1º) En primer lugar, y como ya hemos comentado en la observación, comprobaremos que la función es continua, ya que en caso de no serlo, ya podríamos decir que tampoco es derivable.
2º) Una vez demostrada la continuidad, estudiaremos la existencia de su derivada, para ello comprobaremos que sus derivadas laterales existen y tienen el mismo valor:
Ejemplo 1: Estudiar la derivabilidad de la siguiente función en el punto x=1: 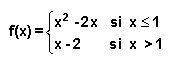
1º) Estudiamos la continuidad en el punto x=1 realizando los límites laterales:
Como los límites laterales coinciden, entonces la función f(x) es continua en el punto de abscisas x=1.
2º) Como la función es continua, pasamos a estudiar la derivabilidad, para ello realizamos como ya hemos comentado, las derivadas laterales:
Como las derivadas laterales no coinciden, entonces f(x) no es derivable.
Observación: Este último paso también se podría haber realizado sin utilizar la definición de derivada, simplemente derivando cada trozo de la función inicial y estudiando de esa manera las derivadas laterales:
INTERPRETACIÓN
Para poder entender gráficamente el significado de la derivabilidad de una función, tendremos en cuenta que cuando una función es continua, pero no es derivable, querrá decir que la función en ese punto tendrá un pico; mientras que en el caso en el que sea continua y derivable será un punto cualquiera de la curva f(x).
Como podemos apreciar en la gráfica de la función del valor absoluto en el punto x=0:
PROPIEDADES DE LAS FUNCIONES DERIVABLES EN UN INTERVALO
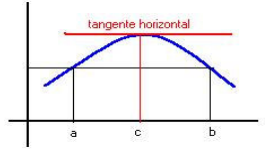
-Teorema de Rolle: Sea f(x) una función continua en el intervalo cerrado [a, b] y derivable en el intervalo abierto (a,b), tal que la función toma el mismo valor en los extremos, es decir f(a)=f(b). Entonces existe un punto perteneciente al intervalo (a,b): c, tal que la derivada en ese punto se anula: f´(c)=0. Lo cual equivale a decir que la tangente en ese punto es horizontal (o paralela al eje de abscisas).
-Teorema del valor medio: Dada una función f(x) continua en el intervalo cerrado [a,b] y continua en el intervalo abierto (a,b), existe un punto c perteneciente al intervalo cerrado tal que: 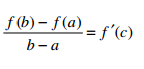
Como podemos observar en la siguiente imagen, significa que existirá un punto de nuestra función en el intervalo (a,b) tal que la tangente en ese punto será paralela al segmento que une el punto (a,f(a)) con el punto (b,f(b)).