Producto mixto
El producto mixto de los vectores U, V y W es igual al producto escalar del primer vector por el producto vectorial de los otros dos. El producto escalar, también conocido como producto interno, es una aplicación externa bilineal definida sobre un espacio vectorial, cuyo resultado al operar entre sí dos vectores, es un escalar o número.
El producto mixto se representa por:
![]()
![]()
El producto mixto de tres vectores dados en función de los versores cartesianos, (un vector unitario o versor es un vector de módulo uno) es igual al determinante que tiene por filas las coordenadas de dichos vectores respecto a una base ortonormal( una base ortonormal es un conjunto de elementos cuyo espacio vectorial generado es denso en el espacio, en el que los elementos son recíprocamente ortogonales y normales, es decir, de magnitud unitaria) El producto mixto de tres vectores es entonces el determinante de la matriz definida por las componentes cartesianas de los tres vectores.
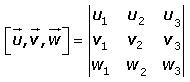
Veamos los siguientes ejemplos:
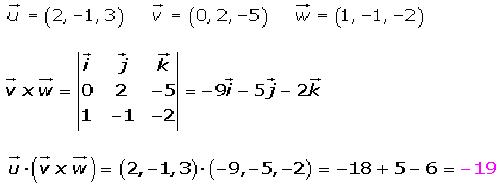
Volumen del paralelepípedo
El valor absoluto (el valor absoluto o módulo de un número real es su valor numérico sin tener en cuenta su signo) del producto mixto representa el volumen del paralelepípedo cuyas aristas son tres vectores que concurren en un mismo vértice (un paralelepípedo es un poliedro de seis caras. Un poliedro es un cuerpo geométrico cuyas caras son planas y encierran un volumen finito)
Hallaremos ahora el volumen de un paralelepípedo, formado con los vectores que siguen a continuación:
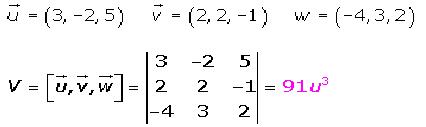
Volumen de un tetraedro
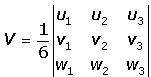
El volumen de un tetraedro (poliedro de cuatro caras) es igual a 1/6 del producto mixto, en valor absoluto.
Obtenemos ahora el volumen del tetraedro cuyos vértices son los puntos A(3, 2, 1), B(1, 2, 4), C(4, 0, 3) y D(1, 1, 7).
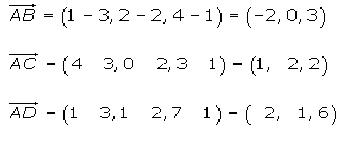
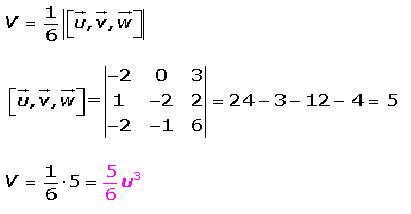
Propiedades del producto mixto
• El producto mixto no varía si varían circularmente sus factores, pero cambia de signo si éstos se trasponen.
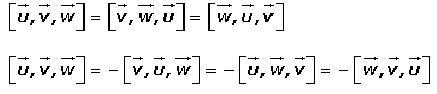
• Una consecuencia inmediata de la interpretación geométrica del producto mixto es la condición de coplanaridad o dependencia lineal de tres vectores del espacio, que se expresa por la anulación de su producto mixto. O sea que si tres vectores son linealmente dependientes ( coplanarios) el producto mixto será 0.
