Aproximación de un número real
Los números reales son aquellos que incluyen a los números racionales (por ejemplo: 40, 38/22, 26,5) como a los irracionales o aquellos que no pueden enunciarse en forma de fracciones y que también tienen infinitas cifras decimales no periódicas, por lo que jamás se van a poder dar en totalidad todas sus cifras decimales, en cambio solo podemos dar una cantidad determinada de ellas. Si sabemos por ejemplo que la raíz cuadrada de 2 es 1.414213562… damos solamente las primeras nueve cifras decimales. Aproximar un número a ciertas cifras decimales es tratar de hallar un número con las cifras pedidas que esté próximo al número dado.
En la aproximación por defecto buscaremos el número con un determinado número de cifras que sea inmediatamente menor al proporcionado. En la aproximación por exceso se busca el número con las cifras decimales fijadas que sea inmediatamente mayor. Por ejemplo dado el número 1.3456, por defecto la aproximación sería 1.34 mientras que por exceso sería 1.35. Pero al dar la aproximación en lugar del número se cometerá un error, en el anterior ejemplo los errores cometidos son los siguientes:
1.3456 – 1.34 = 0.0056
1.3456 – 1.35 = 0.0044
La notación científica, consiste en dar el numero como producto de un numero con solamente una cifra antes de la coma, y una potencia de diez que nos dice cuantos ceros posee el número.Veamos un ejemplo:
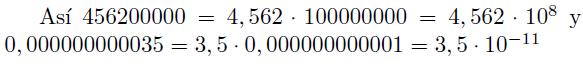
Si tenemos con certeza un determinado número de cifras exactas de un número real, podemos facilitar una aproximación de ese número de menos cifras de dos maneras, por truncamiento o redondeo. En el truncamiento se corta el número a partir de determinada cifra, por ejemplo:

En el redondeo cortamos el número a partir de una determinada cifra, pero además de eso también sumamos uno a la última cifra que surja. En caso de que la primera cifra que excluyamos sea mayor o igual a 5. Por ejemplo:

SI aproximamos un número a por otro b, estamos entonces cometiendo un error (a-b). Si a es un número irracional o sea con infinita cifras decimales, y b es entonces su redondeo o truncamiento, (a-b) será nuevamente un número irracional. Por lo tanto no se puede dar la cifra con exactitud, pero se puede resumir, dando un número que lo limite. Llamaremos a dicho número error absoluto. El error absoluto es la diferencia entre el valor de la medida y el valor tomado como exacto, el cual puede ser negativo o positivo, depende si la medida es superior o no al valor real.
Mientras tanto el error relativo es el resultado de la división o sea el cociente entre el error absoluto y el valor exacto. Si lo multiplicamos por 100 obtendremos el porcentaje de error. Este al igual que el error absoluto puede ser negativo o positivo y puede que sea por exceso o por defecto.
Las cifras significativas de una medida están formadas por los dígitos que se saben no están afectados por el error, más una cifra sometida en este caso al error de la medida. Por ejemplo dada la medida 4, 27 m, serán significativas las cifras, 4, 2, y 7, pero los dígitos 4 y 2 son las cifras exactas mientras el dígito 7 puede ser erróneo.
