Transposición de terminos

Las ecuaciones de primer grado son aquellas que se componen de dos expresiones matemáticas que se unen por el signo de igual. A la expresión que se encuentra a la izquierda del signo la llamaremos primer miembro, mientras a la expresión que se encuentra a la derecha la llamaremos segundo miembro. Para resolver ecuaciones de primer grado las cuales también podemos llamar ecuaciones lineales debemos en primer lugar quitar paréntesis y simplificar, luego quitar denominadores si es que los hay y simplificar, para luego proceder a la transposición de términos. Por ultimo despejamos el coeficiente de la incógnita y simplificamos. Esto consiste en trasladar al otro miembro el coeficiente que acompaña a esta, ya que el que multiplica pasa al otro miembro y viceversa.

Llamaremos transposición de términos a una técnica que nos permite poder solucionar ecuaciones de forma simple. La transposición de términos nos permite agrupar en un miembro todos los términos con x, y en otro los términos que son independientes. Para solucionar ecuaciones, podemos proceder a eliminar términos, por medio de la suma o la resta, multiplicando o dividiendo (por números que sean distintos de cero) en los dos miembros. Para simplificar este proceso podemos hacer que un término que figura en un miembro aparezca de forma inversa al otro, o sea, si se está sumando en un miembro, en el otro se restará, y si se está restando aparecerá sumando. O sea en que en la transposición de la suma el número del primer término que está sumando lo llevaremos al segundo termino restando, luego restaremos ambos números en el segundo termino, dando así la solución y viceversa en el caso de la transposición de una diferencia. Observemos entonces los siguientes ejemplos:

Si se está multiplicando en un miembro, en el otro se aparecerá dividiendo, y si se está dividiendo en el otro se multiplicará.o sea que en la transposición de un producto el número del primer término es decir el que está multiplicando lo llevamos al segundo término dividiendo, luego realizamos el cociente, obteniendo la solución, lo mismo pasa en la transposición de un cociente pero de forma inversa, observemos los siguientes ejemplos:

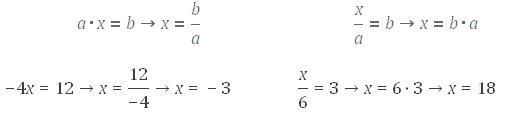
(En estos ejemplo a y b son los términos independientes mientras x es la incógnita de la ecuación)