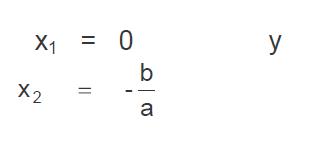Ecuaciones de segundo grado incompletas

Sabemos que las ecuaciones cuadráticas completas son aquellas que tienen todos sus elementos o sea el coeficiente de la variable al cuadrado, el coeficiente de la variable lineal y el término independiente, a la vez estos elementos son distintos de cero. Pero también hay otro tipo de ecuaciones que son las ecuaciones de segundo grado incompletas o cuadráticas incompletas las cuales carecen de uno de sus términos. En caso de que carezcan del termino lineal las denominamos incompletas mixtas, en cambio si carecen del término independiente las denominamos incompletas puras. La forma de llegar a la resolución en este tipo de ecuaciones es diferente en ambos casos.

Para resolver ecuaciones de segundo grado incompletas mixtas debemos colocar ambos términos en el primer miembro de la igualdad. Sacar luego el factor común, igualar a cero los factores y de esta forma obtener las soluciones despejando. Por otro lado para resolver ecuaciones de segundo grado incompletas puras debemos pasar el término independiente al segundo miembro de la igualdad, si este se encuentra en el primer miembro. Luego proceder a despejar la “x” si esto fuera necesario. Como último paso llegamos a la solución sacando la raíz cuadrada. Es posible también resolver una ecuación incompleta in necesidad de emplear la formula general, despejando solamente.

Forma incompleta pura

Como ya hemos mencionado, estas ecuaciones carecen del término que se eleva a la primera potencia, para su resolución debemos operar de la siguiente forma:

Generalmente se dice que las ecuaciones cuadráticas puras tienen dos soluciones correspondientes a números simétricos, por ende en algunos casos la raíz será imaginaria. Decimos que es una raiz imaginaria ya que es la raíz de un número negativo, y al no existir ningún número en el conjunto de números reales que multiplicado por si mismo sea negativo, existe solo en un plano imaginario, entrando así en los números complejos. veamos el siguiente ejemplo:

Comprobaremos ahora con la cifra +6:

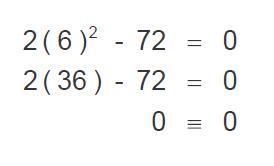
Veamos entonces que sucede con -6:

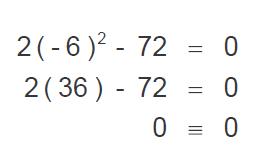
Hemos mencionado también la forma incompleta mixta que es aquella que no tiene el término independiente. El camino o procedimiento para llegar a solucionar una ecuación de este tipo es por medio de la factorización, observemos el siguiente ejemplo:

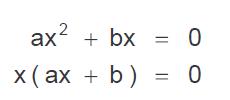
Para que un producto de factores sea cero, cada uno de los factores o por lo menos uno de ellos deberá ser cero, por lo tanto, al igualar el primer factor a cero se obtendrá el siguiente tipo de resultado:

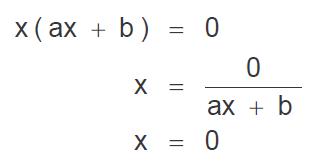
Si igualamos el segundo factor a cero, nos quedará entonces de la siguiente forma:

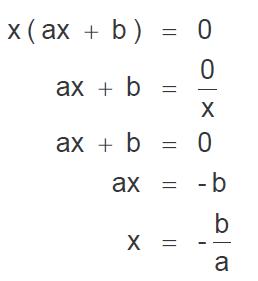
Por lo cual las raíces de esta ecuación incompleta mixta son: